LeetCode每日一题--3月及以前
记录每日一题
2022.11.4
754.到达终点数字
题干
在一根无限长的数轴上,你站在0的位置,终点在target的位置。
你可以做一些数量的移动 numMoves :
- 每次你可以选择向左或向右移动。
- 第 i 次移动(从 i == 1 开始,到 i == numMoves ),在选择的方向上走 i 步。
给定整数 target ,返回:到达目标所需的最小移动次数(即最小 numMoves)
示例
输入: target = 2
输出: 3
解释:
第一次移动,从 0 到 1; 第二次移动,从 1 到 -1; 第三次移动,从 -1 到 2 。输入: target = 3
输出: 2
解释:
第一次移动,从 0 到 1; 第二次移动,从 1 到 3 。解法
本题主要偏向于数学计算,代码性不强。
首先target关于0对称,因此正负与numMoves无关,为便于计算,将target统一为正数。
分析从最简单的情况开始:
- 向右走numMoves步
- 未达到target。那就继续走。
- 正好达到target。此时numMoves为最小值,return。
- 越过了target。
- 越过target后,到达dist。同有三种情况
- dist与target差值为偶数,最好解决,只需要将某些步的方向变为左,一加变一减,就可以弥补差值,正好到达target。此时返回值不变,仍为 numMoves 。
- 差值为奇数,此时需要 numMoves++ ,多走一步,若差值变为偶数(此时差值为奇数,走的步长也为奇数,和就是偶数),则问题转化为上1,返回值为 numMoves + 1 。
- 多走一步,差值仍为奇数,此时再走一步,差值必然变为偶数(同上,走两步的步长必然是一奇一偶,奇数+奇数必是偶数),转化为上1,返回值为numMoves + 2。
以上,代码转化为判断numMoves当前的步长和是否越过了target,以及越过后与target的差值的奇偶。
代码
int reachNumber(int target) {
target = abs(target);
int dist = 0, numMoves = 0;
while(dist < target || (dist - target) % 2){
numMoves++;
dist += numMoves;
}
return numMoves;
}优化
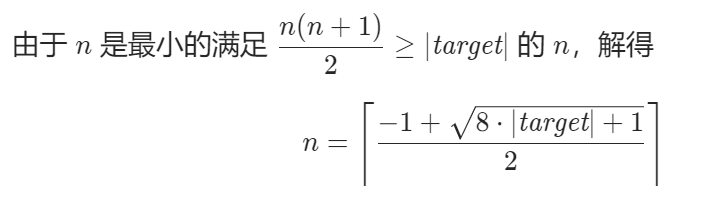
int reachNumber(int target) {
target = abs(target);
int n = ceil((-1 + sqrt(8L * target + 1)) / 2); // 注意 8*target 会超过 int 范围
return (n * (n + 1) / 2 - target) % 2 == 0 ? n : n + 1 + n % 2;
}2022.11.7
816.模糊坐标
题干
我们有一些二维坐标,如 “(1, 3)” 或 “(2, 0.5)”,然后我们移除所有逗号,小数点和空格,得到一个字符串S。返回所有可能的原始字符串到一个列表中。
原始的坐标表示法不会存在多余的零,所以不会出现类似于**”00”, “0.0”, “0.00”, “1.0”, “001”, “00.01”或一些其他更小的数来表示坐标。此外,一个小数点前至少存在一个数,所以也不会出现“.1”**形式的数字。
最后返回的列表可以是任意顺序的。而且注意返回的两个数字中间(逗号之后)都有一个空格。
示例
示例 1:
输入: "(123)"
输出: ["(1, 23)", "(12, 3)", "(1.2, 3)", "(1, 2.3)"]示例 2:
输入: "(00011)"
输出: ["(0.001, 1)", "(0, 0.011)"]
解释: 0.0, 00, 0001 或 00.01 是不被允许的。示例 3:
输入: "(100)"
输出: [(10, 0)]
解释: 1.0 是不被允许的解法
本题实际是两次二分,先将字符串用 “, ” 分为两部分,再用 “.” 分别插入到这两部分中的每个位置,判断是否为一个符合要求的字符串。
最简单的暴力解法:
- for循环从每个位置将字符串分为A、B两部分;
- 对每个A、B,再次for循环从每个位置插入 “.” ,将符合要求的字符串分别存入vector;
- 最后用双for循环从两个vector中取值排列组合,存入返回值的vector中。
仅在插入 “.” 时,需要考虑以下异常情况:
- 若A、B为 “0” 或首位非0,则其整体为一个有效字符串存储。
- for循环插入小数点时,若遇到首位为0时,仅允许在0后插入。
- for循环插入小数点时,若遇到末位为0时,不允许插入。
有限状态机:
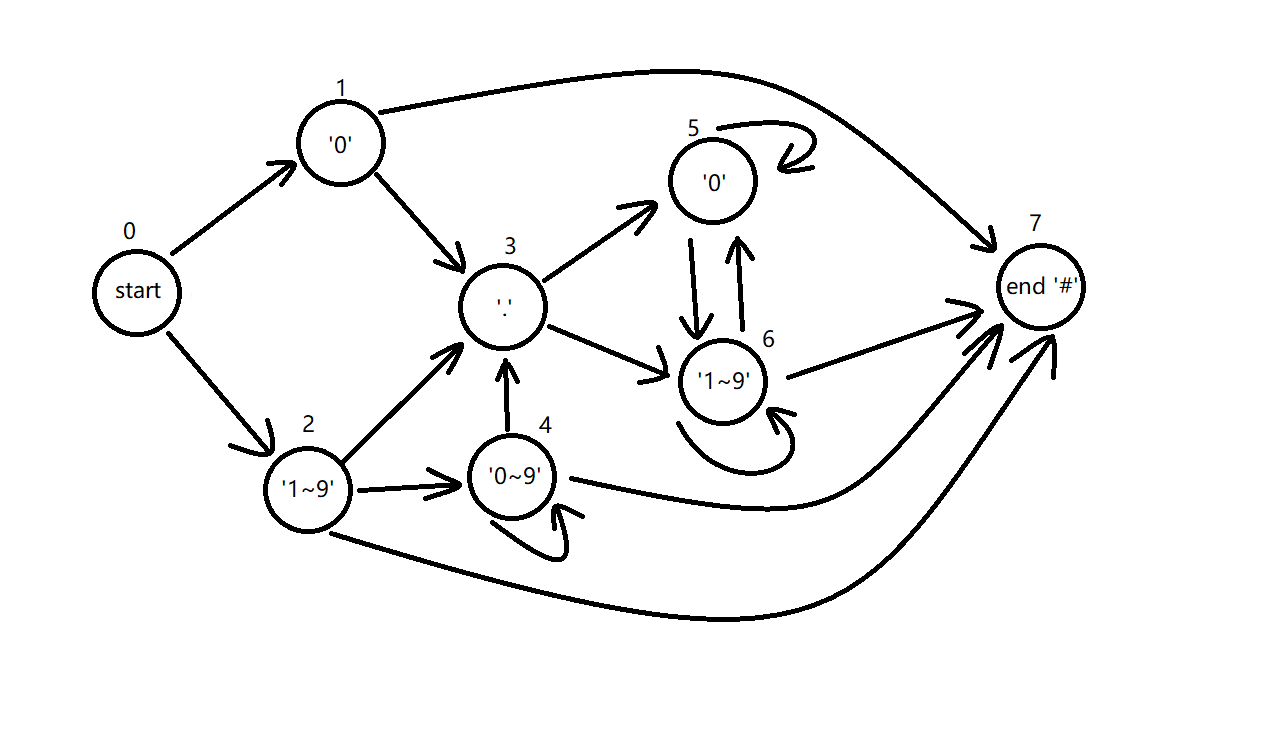
代码
class Solution {
public:
vector<string> classifyNumber(string s){
vector<string> rst;
if(s == "0" || s[0] != '0') rst.push_back(s);
for(int i = 1; i < s.size(); ++i){
if(i != 1 && s[0] == '0' || s.back() == '0') continue;
rst.push_back(s.substr(0, i) + "." + s.substr(i));
}
return rst;
}
vector<string> ambiguousCoordinates(string s) {
vector<string> rst;
s = s.substr(1, s.size() - 2);
for(int i = 1; i < s.size(); ++i){
vector<string> lnum = classifyNumber(s.substr(0, i));
if(lnum.empty()) continue;
vector<string> rnum = classifyNumber(s.substr(i));
if(rnum.empty()) continue;
for(int i = 0; i < lnum.size(); i++){
for(int j = 0; j < rnum.size(); j++){
rst.push_back("(" + lnum[i] + ", " + rnum[j] + ")");
}
}
}
return rst;
}
};for循环中,相比于**++i,i++需要多开辟一个临时变量来存储i自加后的值**,因此前者性能更好。
2022.11.8
1684.统一一致字符串的数目
题干
给你一个由不同字符组成的字符串 allowed 和一个字符串数组 words 。如果一个字符串的每一个字符都在 allowed 中,就称这个字符串是 一致字符串 。
请你返回 words 数组中 一致字符串 的数目。
示例
示例 1:
输入:allowed = "ab", words = ["ad","bd","aaab","baa","badab"]
输出:2
解释:字符串 "aaab" 和 "baa" 都是一致字符串,因为它们只包含字符 'a' 和 'b' 。示例 2:
输入:allowed = "abc", words = ["a","b","c","ab","ac","bc","abc"]
输出:7
解释:所有字符串都是一致的。示例 3:
输入:allowed = "cad", words = ["cc","acd","b","ba","bac","bad","ac","d"]
输出:4
解释:字符串 "cc","acd","ac" 和 "d" 是一致字符串。解法
本题实际是如何判断一个字符串中的每个字符是否都在另一个字符串中出现过的问题。
最简单的暴力解法就是循环words中字符串的每个字符与allowed中的每个字符进行比较,看是否都能匹配上,全匹配上了计数加一。有无法匹配到的跳出循环,判断该字符串为不一致。
解法2:位运算
定义一个32位的int变量,26个字符,各占一位,占据低26位;通过将字符与 ‘a’ 作差计算相应字符需要向左移位多少。某一位为1,表示该位对应的字符存在。
计算出allowed字符串对应的int值standard,和words中的每个字符串对应的值作或运算,若仍为standard原值,说明该字符串的字符均在allowed中,计数num++。
相比于暴力循环,在内存消耗差不多的情况下,提高了1/3速度。
代码
class Solution {
public:
int countConsistentStrings(string allowed, vector<string>& words) {
int num = 0;
auto convert = [](string& str){
int rst = 0;
for(int i = 0; i < str.length(); ++i){
rst |= 1 << (str[i] - 'a');
}
return rst;
};
int standard = convert(allowed);
for(int i = 0; i < words.size(); ++i){
if (standard == (standard | convert(words[i])))
num++;
}
return num;
}
};这里使用了匿名函数的方式来封装统一的转换方法。好处是可以免去函数的声明和定义。这样匿名函数仅在调用函数的时候才会创建函数对象,而调用结束后立即释放,所以匿名函数比非匿名函数更节省空间。
2022.11.9
764.最大加号标志
题干
在一个 n x n 的矩阵 grid 中,除了在数组 mines 中给出的元素为 0,其他每个元素都为 1。**mines[i] = [xi, yi]**表示 grid[xi][yi] == 0
返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
示例
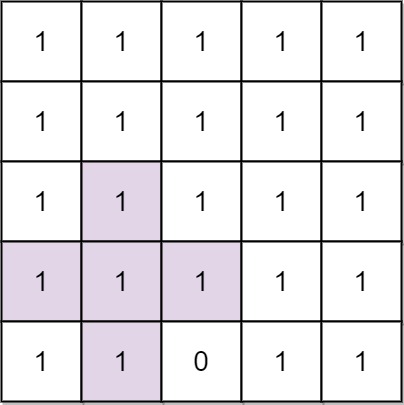
示例 1:
输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
示例 2:
输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志,返回 0 。解法
本题实际是一个动态规划问题。动态规划的核心思想就是——拆分子问题,记住过往,减少重复计算
题中要求十字的最大阶数,但实际上最大阶数是由中心到四个方向上的连续1数量中的最小值决定的。那么问题转变为了:先求每个点为中心到四个方向上的连续1数量中的最小值,再从中取最大值。
如何求四个方向的最小值?假设简化一下,只求左方向的值怎么求?只需要计算每个点左边最长的连续1的格子数,那么十字就是上述的四次重复。初始化时先假设每个点连续1的数量均为网格的宽度n(即最大值),维护一个自加变量left记录连续1的数量。当在一行中从左向右遍历时,如果遇到0,自加变量清零,否则left++。每次自加后与原先该点记录的值取最小值,更新该点的值。
在重复时,同一个点都会经过四个方向的遍历,但只会保留到四个方向里面的最小值了。遍历结束后,得到一个二维的记录每个点最大十字阶数的向量,取里面的最大值即可。
代码
class Solution {
public:
int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
// 初始化矩阵
vector<vector<int> > grid(n, vector<int>(n, n));
for(int i = 0; i < mines.size(); ++i)
grid[mines[i][0]][mines[i][1]] = 0;
// 遍历
int left, right, top, bottom;
for(int i = 0; i < n; ++i){
left = 0; right = 0; top = 0; bottom = 0;
for(int j = 0, k = n - 1; j < n; ++j, --k){
left = grid[i][j] ? left + 1 : 0;
right = grid[i][k] ? right + 1 : 0;
top = grid[j][i] ? top + 1 : 0;
bottom = grid[k][i] ? bottom + 1 : 0;
grid[i][j] = left < grid[i][j] ? left : grid[i][j];
grid[i][k] = right < grid[i][k] ? right : grid[i][k];
grid[j][i] = top < grid[j][i] ? top : grid[j][i];
grid[k][i] = bottom < grid[k][i] ? bottom : grid[k][i];
}
}
int max = 0;
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j){
if (max < grid[i][j]) max = grid[i][j];
}
}
return max;
}
};注:vector的初始化方式。
vector采用
for(auto& item : vector)的形式遍历较为方便,但是速度较普通for循环更慢,但是不用担心越界问题。
2022.11.11
1704.判断字符串的两半是否相似
题干
给你一个偶数长度的字符串 s 。将其拆分成长度相同的两半,前一半为 a ,后一半为 b 。
两个字符串 相似 的前提是它们都含有相同数目的元音(**’a’,’e’,’i’,’o’,’u’,’A’,’E’,’I’,’O’,’U’)。注意,s** 可能同时含有大写和小写字母。
如果 a 和 b 相似,返回 true ;否则,返回 false 。
示例
示例 1:
输入:s = "book"
输出:true
解释:a = "bo" 且 b = "ok" 。a 中有 1 个元音,b 也有 1 个元音。所以,a 和 b 相似。示例 2:
输入:s = "textbook"
输出:false
解释:a = "text" 且 b = "book" 。a 中有 1 个元音,b 中有 2 个元音。因此,a 和 b 不相似。解法
本题实际就是一次for循环,对字符串s的每个字符判断一次是否为元音即可,中间记录下前后半的元音个数。
可优化的点在于
1.不必for循环整个字符串,由于a、b长度相同,可以只for循环前一半(类似双指针?)。
2.只需维护一个变量记录元音数量即可,左加右减,节约内存。
代码
class Solution {
public:
bool halvesAreAlike(string s) {
auto isVowel = [](char c){
int val = c - 'A';
if (val == 0 || val == 4 || val == 8 || val == 14 || val == 20
|| val == 32 || val == 36 || val == 40 || val == 46 || val == 52 )
return true;
else
return false;
};
int cnt = 0;
int len = s.length() / 2;
for(int i = 0; i < len; ++i){
cnt += isVowel(s[i]) ? 1 : 0;
cnt -= isVowel(s[i + len]) ? 1 : 0;
}
return cnt == 0;
}
};我这里直接写了个匿名函数通过ASCII的差值判断是否为元音,还可以用集合。
unordered_set<char> vowels = {'a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'};
cnt += vowels.count(s[i]);2022.12.6
1805.字符串中不同整数的数目
题干
给你一个字符串 word ,该字符串由数字和小写英文字母组成。
请你用空格替换每个不是数字的字符。例如,**”a123bc34d8ef34”** 将会变成 “ 123 34 8 34” 。注意,剩下的这些整数为(相邻彼此至少有一个空格隔开):**”123”、”34”、”8”** 和 “34” 。
返回对 word 完成替换后形成的 不同 整数的数目。
只有当两个整数的 不含前导零 的十进制表示不同, 才认为这两个整数也不同。
示例
示例 1:
输入:word = "a123bc34d8ef34"
输出:3
解释:不同的整数有 "123"、"34" 和 "8" 。注意,"34" 只计数一次。示例 2:
输入:word = "leet1234code234"
输出:2示例 3:
输入:word = "a1b01c001"
输出:1
解释:"1"、"01" 和 "001" 视为同一个整数的十进制表示,因为在比较十进制值时会忽略前导零的存在。解法
本题解法就是双指针和C++集合不能有重复项特点的应用。
先用一个头指针 i ,for循环遍历字符串的每一项,判断是否为数字(ASCII码值小于58,09是4857),如果为数字,进行三步操作:
1.使用另一个指针 j ,从 i 处开始向后扫,直到扫到非数字字符。
2.移动 i ,从该串数字的最高位开始判断有无0,有前导0的位全部去掉。
3.将过滤后的字符串加入集合Set中。
代码
class Solution {
public:
int numDifferentIntegers(string word) {
set<string> nums;
int j, len = word.length();
for(int i = 0; i < len; i++){
if(word[i] < 58){
j = i;
while(word[j] < 58 && j < len) j++;
while(word[i] == 48 && j - i > 1) i++;
nums.insert(word.substr(i, j - i));
i = j;
}
}
return nums.size();
}
};2022.12.7
1775.通过最少操作次数使数组的和相等
题干
给你两个长度可能不等的整数数组 nums1 和 nums2 。两个数组中的所有值都在 1 到 6 之间(包含 1 和 6)。
每次操作中,你可以选择 任意 数组中的任意一个整数,将它变成 1 到 6 之间 任意 的值(包含 1 和 6)。
请你返回使 nums1 中所有数的和与 nums2 中所有数的和相等的最少操作次数。如果无法使两个数组的和相等,请返回 -1 。
示例
示例 1:
输入:nums1 = [1,2,3,4,5,6], nums2 = [1,1,2,2,2,2]
输出:3
解释:你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums2[0] 变为 6 。 nums1 = [1,2,3,4,5,6], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[5] 变为 1 。 nums1 = [1,2,3,4,5,1], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[2] 变为 2 。 nums1 = [1,2,2,4,5,1], nums2 = [6,1,2,2,2,2] 。示例 2:
输入:nums1 = [1,1,1,1,1,1,1], nums2 = [6]
输出:-1
解释:没有办法减少 nums1 的和或者增加 nums2 的和使二者相等。示例 3:
输入:nums1 = [6,6], nums2 = [1]
输出:3
解释:你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums1[0] 变为 2 。 nums1 = [2,6], nums2 = [1] 。
- 将 nums1[1] 变为 2 。 nums1 = [2,2], nums2 = [1] 。
- 将 nums2[0] 变为 4 。 nums1 = [2,2], nums2 = [4] 。解法
本题用到了贪心思想,即一个问题拆解成多个步骤,每个步骤采用最优的解法。
在本题中,要让两个数组以最少步骤达到和相同,就代表每一步缩小的差距越大越好,也就是**优先把和小的数组里的 1 变成 6 ,把和大的数组中的 6 变成 1.**以此类推,接下来是5、2;4、3······当走到其中一步时差距缩小为非正数时,说明该步就是最后一步了。
并且1变6和6变1的意义是相同的,都是缩小了5的差距,因此从节约空间的角度考虑,可以只维护一个长度为6的1维数组,记录操作的分布情况(缩小543210的差距)。
代码
class Solution {
public:
int minOperations(vector<int>& nums1, vector<int>& nums2) {
int diff = accumulate(nums1.begin(), nums1.end(), 0) - accumulate(nums2.begin(), nums2.end(), 0);
if (diff < 0) return minOperations(nums2, nums1);
if (diff == 0) return 0;
int cnt[6] = {0};
int i = 0, count = 0;
for(;i < nums1.size();++i) ++cnt[nums1[i] - 1];
for(i = 0;i < nums2.size();++i) ++cnt[6 - nums2[i]];
for(i = 5;i > 0; --i){
while(cnt[i] > 0 && diff > 0){
diff -= i;
--cnt[i];
count++;
}
}
return diff > 0 ? -1 : count;
}
};accumulate属于numeric头文件,作用是计算数组或C++容器指定地址范围内的成员的和。
参数1、2分别为 容器 / 数组 指向要计算的第一个元素和最后一个元素的 迭代器 / 首地址 ,参数3为累加的初始值。
这里为了下面for循环存储操作的分布情况,固定了nums1的和要大于nums2;若是小于,就调换输入顺序重新执行函数(这里测试过,相比于swap调换两个vector,这种方式要快一些)。这里心机的把 diff == 0 的情况放在了 diff < 0 下面,大部分情况下应该都是不相等的,这样可以少点计算量(dog)。
2022.12.9
1780.判断一个数字是否可以表示成三的幂的和
题干
给你一个整数 n ,如果你可以将 n 表示成若干个不同的三的幂之和,请你返回 true ,否则请返回 false 。
对于一个整数 y ,如果存在整数 x 满足 y == 3^x ,我们称这个整数 y 是三的幂。
示例
示例 1:
输入:n = 12
输出:true
解释:12 = 3^1 + 3^2示例 2:
输入:n = 91
输出:true
解释:91 = 3^0 + 3^2 + 3^4示例 3:
输入:n = 21
输出:false 解法
基本思路:
看示例1可知,满足条件的数为3的不同次幂的和,那么必然能被3整除,看示例2可知另一情况,3^0为1,也就是除以3余数为1,但是也满足条件。当示例1中除以3,得到4,又变成了示例2的情况,即3^0 + 3的幂。
于是得到满足条件的整数一定具有以下性质:
- 除以3以后余数必为1或0;
- 性质1得到的商依旧满足性质1,直至商为0。
代码
class Solution {
public:
bool checkPowersOfThree(int n) {
while(n){
if (n % 3 == 2) return false;
n /= 3;
}
return true;
}
};2023.2.8
1233.删除子文件夹(未完结)
题干
你是一位系统管理员,手里有一份文件夹列表 folder,你的任务是要删除该列表中的所有 子文件夹,并以 任意顺序 返回剩下的文件夹。
如果文件夹 folder[i] 位于另一个文件夹 folder[j] 下,那么 folder[i] 就是 folder[j] 的 子文件夹 。
文件夹的「路径」是由一个或多个按以下格式串联形成的字符串:**’/‘** 后跟一个或者多个小写英文字母。
例如,”/leetcode“ 和 “/leetcode/problems“ 都是有效的路径,而空字符串和 “/“ 不是。
示例
示例 1:
输入:folder = ["/a","/a/b","/c/d","/c/d/e","/c/f"]
输出:["/a","/c/d","/c/f"]
解释:"/a/b" 是 "/a" 的子文件夹,而 "/c/d/e" 是 "/c/d" 的子文件夹。示例 2:
输入:folder = ["/a","/a/b/c","/a/b/d"]
输出:["/a"]
解释:文件夹 "/a/b/c" 和 "/a/b/d" 都会被删除,因为它们都是 "/a" 的子文件夹。示例 3:
输入: folder = ["/a/b/c","/a/b/ca","/a/b/d"]
输出: ["/a/b/c","/a/b/ca","/a/b/d"]解法
基本思路:
先按照字典序排序(/a,/a/b,/a/b/c,/b),这样在遍历时只需要和上一个被加入的非子文件夹比较(因为相同根文件夹情况下先短后长排序),便于排除。
将第一个文件夹加入输出,遍历folder中的剩余文件夹,作如下判断:
1.当前字符串长度比上一个被加入的字符串短的,必然是根文件夹名改变了,是非子文件夹,加入。
2.当前字符串的前n个字符与上一个被加入的字符串完全相同且第n+1个字符为 ‘/’ 的,必然是子文件夹,排除。
解法2:字典树
代码
class Solution {
public:
vector<string> removeSubfolders(vector<string>& folder) {
sort(folder.begin(), folder.end());
vector<string> rst = {folder[0]};
for(int i = 1; i < folder.size(); ++i){
int ori_len = rst.back().size();
int cur_len = folder[i].size();
if (ori_len >= cur_len || !(rst.back() == folder[i].substr(0, ori_len) && folder[i][ori_len] == '/'))
rst.push_back(folder[i]);
}
return rst;
}
};2023.2.9
1797.设计一个验证系统
题干
你需要设计一个包含验证码的验证系统。每一次验证中,用户会收到一个新的验证码,这个验证码在 currentTime 时刻之后 timeToLive 秒过期。如果验证码被更新了,那么它会在 currentTime (可能与之前的 currentTime 不同)时刻延长 timeToLive 秒。
请你实现 AuthenticationManager 类:
- AuthenticationManager(int timeToLive) 构造 AuthenticationManager 并设置 timeToLive 参数。
- generate(string tokenId, int currentTime) 给定 tokenId ,在当前时间 currentTime 生成一个新的验证码。
- renew(string tokenId, int currentTime) 将给定 tokenId 且 未过期 的验证码在 currentTime 时刻更新。如果给定 tokenId 对应的验证码不存在或已过期,请你忽略该操作,不会有任何更新操作发生。
- countUnexpiredTokens(int currentTime) 请返回在给定 currentTime 时刻,未过期 的验证码数目。
- 如果一个验证码在时刻 t 过期,且另一个操作恰好在时刻 t 发生(renew 或者 countUnexpiredTokens 操作),过期事件 优先于 其他操作。
- 所有
generate函数的调用都会包含独一无二的tokenId值。 - 所有函数调用中,
currentTime的值 严格递增 。 - 所有函数的调用次数总共不超过
2000次。
示例
输入:
["AuthenticationManager", "renew", "generate", "countUnexpiredTokens", "generate", "renew", "renew", "countUnexpiredTokens"]
[[5], ["aaa", 1], ["aaa", 2], [6], ["bbb", 7], ["aaa", 8], ["bbb", 10], [15]]
输出:
[null, null, null, 1, null, null, null, 0]
解释:
AuthenticationManager authenticationManager = new AuthenticationManager(5); // 构造 AuthenticationManager ,设置 timeToLive = 5 秒。
authenticationManager.renew("aaa", 1); // 时刻 1 时,没有验证码的 tokenId 为 "aaa" ,没有验证码被更新。
authenticationManager.generate("aaa", 2); // 时刻 2 时,生成一个 tokenId 为 "aaa" 的新验证码。
authenticationManager.countUnexpiredTokens(6); // 时刻 6 时,只有 tokenId 为 "aaa" 的验证码未过期,所以返回 1 。
authenticationManager.generate("bbb", 7); // 时刻 7 时,生成一个 tokenId 为 "bbb" 的新验证码。
authenticationManager.renew("aaa", 8); // tokenId 为 "aaa" 的验证码在时刻 7 过期,且 8 >= 7 ,所以时刻 8 的renew 操作被忽略,没有验证码被更新。
authenticationManager.renew("bbb", 10); // tokenId 为 "bbb" 的验证码在时刻 10 没有过期,所以 renew 操作会执行,该 token 将在时刻 15 过期。
authenticationManager.countUnexpiredTokens(15); // tokenId 为 "bbb" 的验证码在时刻 15 过期,tokenId 为 "aaa" 的验证码在时刻 7 过期,所有验证码均已过期,所以返回 0 。解法
基本思路:
采用哈希表存储 [tokenId,过期时间点] 这一键值对,保存信息。
因为提到了currentTime是严格递增的,因此在存储id时可以不用队列,直接用顺序表存储。
因为函数总调用次数不超过2000次,因此甚至不需要对表进行维护(即删除过期id)。
代码
class AuthenticationManager {
public:
AuthenticationManager(int timeToLive) {
liveTime = timeToLive;
}
void generate(string tokenId, int currentTime) {
liveIds[tokenId] = currentTime + liveTime;
}
void renew(string tokenId, int currentTime) {
if (liveIds[tokenId] > currentTime)
generate(tokenId, currentTime);
}
int countUnexpiredTokens(int currentTime) {
int cnt = 0;
for (auto iter = liveIds.begin(); iter != liveIds.end(); ++iter) {
if (iter->second > currentTime)
cnt++;
}
return cnt;
}
private:
int liveTime;
unordered_map<string, int> liveIds;
};
/**
* Your AuthenticationManager object will be instantiated and called as such:
* AuthenticationManager* obj = new AuthenticationManager(timeToLive);
* obj->generate(tokenId,currentTime);
* obj->renew(tokenId,currentTime);
* int param_3 = obj->countUnexpiredTokens(currentTime);
*/2023.2.11
2335.装满杯子所需的最短总时长
题干
现有一台饮水机,可以制备冷水、温水和热水。每秒钟,可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。
给你一个下标从 0 开始、长度为 3 的整数数组 amount ,其中 amount[0]、amount[1] 和 amount[2] 分别表示需要装满冷水、温水和热水的杯子数量。返回装满所有杯子所需的 最少 秒数。
示例
示例 1:
输入:amount = [1,4,2]
输出:4
解释:下面给出一种方案:
第 1 秒:装满一杯冷水和一杯温水。
第 2 秒:装满一杯温水和一杯热水。
第 3 秒:装满一杯温水和一杯热水。
第 4 秒:装满一杯温水。
可以证明最少需要 4 秒才能装满所有杯子。示例 2:
输入:amount = [5,4,4]
输出:7示例 3:
输入:amount = [5,0,0]
输出:5解法
基本思路:
简单的贪心算法。每次循环先排序,取较大的两个各减一,直至全为0.
代码
class Solution {
public:
int fillCups(vector<int>& amount) {
int turns = 0;
while(amount[0] + amount[1] + amount[2]) {
sort(amount.begin(), amount.end());
turns++;
amount[2]--;
if (amount[1] > 0)
amount[1]--;
}
return turns;
}
};2023.2.13
1234.替换子串得到平衡字符串
题干
有一个只含有 ‘Q’, ‘W’, ‘E’, ‘R’ 四种字符,且长度为 n 的字符串。
假如在该字符串中,这四个字符都恰好出现 n/4 次,那么它就是一个「平衡字符串」。
给你一个这样的字符串 s,请通过「替换一个子串」的方式,使原字符串 s 变成一个「平衡字符串」。
你可以用和「待替换子串」长度相同的 任何 其他字符串来完成替换。
请返回待替换子串的最小可能长度。
如果原字符串自身就是一个平衡字符串,则返回 0。
示例
示例 1:
输入:s = "QWER"
输出:0
解释:s 已经是平衡的了。示例 2:
输入:s = "QQWE"
输出:1
解释:我们需要把一个 'Q' 替换成 'R',这样得到的 "RQWE" (或 "QRWE") 是平衡的。示例 3:
输入:s = "QQQQ"
输出:3
解释:我们可以替换后 3 个 'Q',使 s = "QWER"。解法
基本思路:
最终目标是四个字符的数量都达到 n/4 个时,改动字符串的长度怎么取最短。很容易想到双指针来控制应该改动的部分的首尾。
因为替换字符串内的字符都可以任选,那么只要保证该子串外的字符数达标即可。那么判断条件就是子串外的四个字符数均小于等于 n/4 个。
先统计一遍原字符串中的四个字符数。
移动右指针时将子串外对应字符数-1,移动左指针+1。
以右指针为基准进行for循环,通过左指针右移压缩改动字符串的长度,找出符合标准的最小值即可。
代码
class Solution {
public:
int balancedString(string s) {
int len = s.length();
int num = len / 4, cnt['X'] = {0};
for (char& c : s) {
cnt[c]++;
}
if (cnt['Q'] == num && cnt['W'] == num && cnt['E'] == num && cnt['R'] == num)
return 0;
int res = len, left = 0;
for (int right = 0; right < len; ++right) {
cnt[s[right]]--;
while (left <= right && cnt['Q'] <= num && cnt['W'] <= num && cnt['E'] <= num && cnt['R'] <= num) {
res = min(res, right - left + 1);
cnt[s[left++]]++;
}
}
return res;
}
};2023.2.18
1237.找出给定方程的正整数解
题干
给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)
f(x, y) < f(x, y + 1)
函数接口定义如下:
interface CustomFunction {
public:
// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.
int f(int x, int y);
};你的解决方案将按如下规则进行评判:
- 判题程序有一个由 CustomFunction 的 9 种实现组成的列表,以及一种为特定的 z 生成所有有效数对的答案的方法。
- 判题程序接受两个输入:function_id(决定使用哪种实现测试你的代码)以及目标结果 z 。
- 判题程序将会调用你实现的 findSolution 并将你的结果与答案进行比较。
- 如果你的结果与答案相符,那么解决方案将被视作正确答案,即 Accepted 。
示例
示例 1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5示例 2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5提示:
- 1 <= function_id <= 9
- 1 <= z <= 100
- 题目保证 f(x, y) == z 的解处于 1 <= x, y <= 1000 的范围内。
- 在 1 <= x, y <= 1000 的前提下,题目保证 f(x, y) 是一个 32 位有符号整数。
解法
基本思路:
这个题目我觉得题干有非常多的无效信息,因为f(x,y)是具体实现不可见的函数。
实际有效的信息只有两条:
- f(x,y)是单调递增函数
- x,y的取值范围均为 [1, 1000]
那么我们可以采用枚举的方式(遍历),分别将x,y的值设为区间的两端(原因后面可以体会到)
x初始为1最小,y初始为1000最大(即x只能递增,y只能递减),计算f(x,y)有三种结果
- 当f(x,y)< z 时,由单调性可知,f(x,y-1)同样小于z,而我们的目标是等于z,此时唯一的动作就是x++;
- 当f(x,y)> z 时,同理,只能y–;
- 当f(x,y)== z 时,存储这一对x,y,同时x++,y–(两个同时增减,因为只变动一个没有意义,必然不可能等于z)。
代码
/*
* // This is the custom function interface.
* // You should not implement it, or speculate about its implementation
* class CustomFunction {
* public:
* // Returns f(x, y) for any given positive integers x and y.
* // Note that f(x, y) is increasing with respect to both x and y.
* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)
* int f(int x, int y);
* };
*/
class Solution {
public:
vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
vector<vector<int>> res;
int x = 1, y = 1000;
while(x <= 1000 && y) {
int rst = customfunction.f(x, y);
if (rst < z)
x++;
else if (rst > z)
y--;
else
res.push_back({x++, y--});
}
return res;
}
};2023.2.20
2347.最好的扑克手牌
题干
给你一个整数数组 ranks 和一个字符数组 suit 。你有 5 张扑克牌,第 i 张牌大小为 ranks[i] ,花色为 suits[i] 。
下述是从好到坏你可能持有的 手牌类型 :
- “Flush“:同花,五张相同花色的扑克牌。
- “Three of a Kind“:三条,有 3 张大小相同的扑克牌。
- “Pair“:对子,两张大小一样的扑克牌。
- “High Card“:高牌,五张大小互不相同的扑克牌。
请你返回一个字符串,表示给定的 5 张牌中,你能组成的 最好手牌类型 。
示例
示例 1:
输入:ranks = [13,2,3,1,9], suits = ["a","a","a","a","a"]
输出:"Flush"示例 2:
输入:ranks = [4,4,2,4,4], suits = ["d","a","a","b","c"]
输出:"Three of a Kind"示例 3:
输入:ranks = [10,10,2,12,9], suits = ["a","b","c","a","d"]
输出:"Pair"解法
基本思路:
简单题,没啥说的,翻译一下就是:
- 先判断suits里的元素是否均相同;
- 再判断ranks里是否存在三个/两个/不存在相同的元素;
代码
class Solution {
public:
string bestHand(vector<int>& ranks, vector<char>& suits) {
if (equal(suits.begin()+1, suits.end(), suits.begin()))
return "Flush";
int cnt[14] = {0};
bool isPair = false;
for(int i = 0; i < ranks.size(); ++i){
if(++cnt[ranks[i]] == 3)
return "Three of a Kind";
isPair |= cnt[ranks[i]] == 2;
}
return isPair ? "Pair" : "High Card";
}
};2023.2.24
2357.使数组中所有元素都等于0
题干
给你一个非负整数数组 nums 。在一步操作中,你必须:
- 选出一个正整数 x ,x 需要小于或等于 nums 中 最小 的 非零 元素。
- nums 中的每个正整数都减去 x。
返回使 nums 中所有元素都等于 0 需要的 最少 操作数。
示例
示例 1:
输入:nums = [1,5,0,3,5]
输出:3
解释:
第一步操作:选出 x = 1 ,之后 nums = [0,4,0,2,4] 。
第二步操作:选出 x = 2 ,之后 nums = [0,2,0,0,2] 。
第三步操作:选出 x = 2 ,之后 nums = [0,0,0,0,0] 。示例 2:
输入:nums = [0]
输出:0解法
基本思路:
简单题,没啥说的,每一步都找一个最小的正整数减掉,直到全为0。
不必要真去减,如示例1,第一步减1后3变成2,正好是第二步减的数,也就是说只需要记录之前减的总数(上一个需要被减的数本身)就行。
代码
class Solution {
public:
int minimumOperations(vector<int>& nums) {
sort(nums.begin(), nums.end());
int lastNum = 0, cnt = 0;
for(int i = 0; i < nums.size(); ++i){
if (nums[i] - lastNum > 0) {
lastNum = nums[i];
cnt++;
}
}
return cnt;
}
};2023.2.25
1247.交换字符使得字符串相同
题干
有两个长度相同的字符串 s1 和 s2,且它们其中 只含有 字符 “x“ 和 “y“,你需要通过「交换字符」的方式使这两个字符串相同。
每次「交换字符」的时候,你都可以在两个字符串中各选一个字符进行交换。
交换只能发生在两个不同的字符串之间,绝对不能发生在同一个字符串内部。也就是说,我们可以交换 **s1[i] 和 s2[j]**,但不能交换 **s1[i] 和 s1[j]**。
最后,请你返回使 s1 和 s2 相同的最小交换次数,如果没有方法能够使得这两个字符串相同,则返回 -1 。
示例
示例 1:
输入:s1 = "xx", s2 = "yy"
输出:1
解释:交换 s1[0] 和 s2[1],得到 s1 = "yx",s2 = "yx"。示例 2:
输入:s1 = "xy", s2 = "yx"
输出:2
解释:
交换 s1[0] 和 s2[0],得到 s1 = "yy",s2 = "xx" 。
交换 s1[0] 和 s2[1],得到 s1 = "xy",s2 = "xy" 。示例 3:
输入:s1 = "xx", s2 = "xy"
输出:-1解法
基本思路:
首先统计两个字符串同一位置下的字符不同的数量,因为交换只会发生在不同处。
不同有两种情况,xy和yx。
根据上述三个示例可以得出结论,对于每2对不同的字符:
- 若为同一形式(均为xy),只需要对角交换1次即可相同;
- 若为不同形式(xy和yx),需要先同位置交换1次变为示例1,再对角交换一次;
- 若仅有一对不同,无法交换至相同。
可以得出结论:
- xy、yx和为奇数,无法相同,返回-1;
- 若和为偶数,分为两种情况,xy、yx均为偶数或奇数;
- 若均为偶数,按照每两对1次的情况,只需要 xy / 2 + yx / 2 次
- 若均为奇数,则在除去每两对一次的情况下,会留存一对示例2情况;
- 结合3、4可得共 xy / 2 + yx / 2 + xy % 2 + yx % 2 次。
代码
class Solution {
public:
int minimumSwap(string s1, string s2) {
int xy = 0, yx = 0;
for(int i = 0; i < s1.length(); ++i){
xy += s1[i] < s2[i];
yx += s1[i] > s2[i];
}
if ((xy + yx) % 2)
return -1;
return xy / 2 + yx / 2 + xy % 2 + yx % 2;
}
};2023.2.27
1144.递减元素使数组成锯齿状
题干
给你一个整数数组 nums,每次操作会从中选择一个元素并将该元素的值减少 1。
如果符合下列情况之一,则数组 A 就是 锯齿数组:
- 每个偶数索引对应的元素都大于相邻的元素,即 A[0] > A[1] < A[2] > A[3] < A[4] > …
- 每个奇数索引对应的元素都大于相邻的元素,即 A[0] < A[1] > A[2] < A[3] > A[4] < …
返回将数组 nums 转换为锯齿数组所需的最小操作次数。
示例
示例 1:
输入:nums = [1,2,3]
输出:2
解释:我们可以把 2 递减到 0,或把 3 递减到 1。示例 2:
输入:nums = [9,6,1,6,2]
输出:4解法
基本思路:
枚举呗。
奇数和偶数下标各遍历一遍,每次都判断和两边的差值,记录最大值求和即可。
排除掉当元素处于数组边界时越界的问题,最后比较两种哪种小。
代码
class Solution {
public:
int movesToMakeZigzag(vector<int>& nums) {
int cnt[2] = {0};
for(int i = 0; i < 2; ++i){
for(int j = i; j < nums.size(); ++j, ++j){
int step = 0;
if(j) step = max(step, nums[j] - nums[j - 1] + 1);
if(j < nums.size()-1) step = max(step, nums[j] - nums[j + 1] + 1);
cnt[i] += step;
}
}
return min(cnt[0], cnt[1]);
}
};面试题16.07.最大数值
题干
编写一个方法,找出两个数字 a 和 b 中最大的那一个。不得使用if-else或其他比较运算符。
示例
示例 1:
输入: a = 1, b = 2
输出: 2解法
基本思路:
首先考虑到的就是不用比较符号如何出现控制输出a还是b呢?
想到了类似门电路,用0和1控制就行,也就是 a * (condition ^ 1) + b * condition ;
那么什么运算结果是0和1呢,很容易想到通过位运算获取符号位。
于是得到以下代码:
class Solution {
public:
int maximum(int a, int b) {
// 注意当值为负数时,右移高位是会补1的,因此需要把计算结果转为无符号
int signSub = static_cast<unsigned>(a - b) >> 31;
return a * (signSub ^ 1) + b * signSub;
}
};提交时出现了问题 signed integer overflow: 2147483647 - -2147483648 cannot be represented in type 'int'
忘记考虑了溢出的问题,在 a - b 时就溢出了。当a和b同号时,不存在溢出问题,可以直接用上述方法,只有当ab异号时需要考虑溢出问题。
可以发现,当a和b异号时,若a为负数,符号位1,需要输出b,也就是signSub = 1;a为正数,符号位0,输出a,signSub = 0.
可以得到此时的处理方法,signSub = a符号位 ^ b符号位 ^ b符号位。
在不使用比较运算符的情况下,可以用 && 作为if判断使用。
代码
class Solution {
public:
int maximum(int a, int b) {
int signA = static_cast<unsigned>(a) >> 31;
int signB = static_cast<unsigned>(b) >> 31;
int signSub = signA ^ signB ^ signB;
int temp = (signA ^ signB ^ 1) && (signSub = static_cast<unsigned>(a - b) >> 31);
return a * (signSub ^ 1) + b * signSub;
}
};2023.2.28
2363.合并相似的物品
题干
给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质:
- items[i] = [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,weighti 表示第 i 件物品的 重量 。
- items 中每件物品的价值都是 唯一 的 。
请你返回一个二维数组 ret,其中 **ret[i] = [valuei, weighti]**, weighti 是所有价值为 valuei 物品的 重量之和 。
注意:
ret 应该按价值 升序 排序后返回。
1 <= valuei, weighti <= 1000
示例
示例 1:
输入:items1 = [[1,1],[4,5],[3,8]], items2 = [[3,1],[1,5]]
输出:[[1,6],[3,9],[4,5]]示例 2:
输入:items1 = [[1,1],[3,2],[2,3]], items2 = [[2,1],[3,2],[1,3]]
输出:[[1,4],[2,4],[3,4]]示例 3:
输入:items1 = [[1,3],[2,2]], items2 = [[7,1],[2,2],[1,4]]
输出:[[1,7],[2,4],[7,1]]解法
基本思路:
就是求出现过的每种价值的总重量,价值不重复,自然想到了哈希,开一个 cnt[1001] ,下标表示价值。
刚好,需要按照价值升序排序,从小到大遍历cnt即可。
代码
class Solution {
public:
vector<vector<int>> mergeSimilarItems(vector<vector<int>>& items1, vector<vector<int>>& items2) {
vector<vector<int>> ret;
int cnt[1001] = {0};
for(int i = 0; i < items1.size(); ++i){
cnt[items1[i][0]] += items1[i][1];
}
for(int i = 0; i < items2.size(); ++i){
cnt[items2[i][0]] += items2[i][1];
}
for(int i = 0; i < 1001; ++i){
if(cnt[i])
ret.push_back({i, cnt[i]});
}
return ret;
}
};191.位1的个数
题干
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
提示:输入必须是长度为 32 的 二进制串 。
示例
示例 1:
输入:n = 00000000000000000000000000001011
输出:3示例 2:
输入:n = 11111111111111111111111111111101
输出:31解法
基本思路:
位运算,每位都和1与一下就行。
尝试了一下发现,1移位和n与 ,比 n移位和1与 速度快。
代码
class Solution {
public:
int hammingWeight(uint32_t n) {
int cnt = 0;
for(int i = 0; i < 32; ++i){
if ((n & (1 << i)) > 0)
cnt++;
}
return cnt;
}
};2023.3.1
2373.矩阵中的局部最大值
题干
给你一个大小为 n x n 的整数矩阵 grid 。
生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足:
maxLocal[i] [j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。
换句话说,我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。
返回生成的矩阵
示例
示例 1:
输入:grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出:[[9,9],[8,6]]示例 2:
输入:grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出:[[2,2,2],[2,2,2],[2,2,2]]解法
基本思路:
暴力for循环。。
代码
class Solution {
public:
vector<vector<int>> largestLocal(vector<vector<int>>& grid) {
int size = grid.size();
vector<vector<int>> res(size - 2, vector<int>(size - 2));
for(int i = 0; i < size - 2; ++i){
for(int j = 0; j < size - 2; ++j){
for(int x = i; x < i + 3; ++x){
for(int y = j; y < j + 3; ++y){
res[i][j] = max(res[i][j], grid[x][y]);
}
}
}
}
return res;
}
};2023.3.2
面试题05.02.二进制数转字符串
题干
二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。
如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。
提示:
32位包括输出中的
"0."这两位。题目保证输入用例的小数位数最多只有
6位
示例
示例 1:
输入:0.625
输出:"0.101"示例 2:
输入:0.1
输出:"ERROR"
提示:0.1无法被二进制准确表示解法
基本思路:
double小数的二进制转化方法,以0.625为例:
- 0.625 * 2 = 1.25,取整数位1作为小数点后第一位;
- (1.25 - 1)* 2 = 0.5,取整数位0作为小数点后第二位;
- 0.5 * 2 = 1,取整数位1作为小数点后第三位;
- 此时剩余数1 - 1 = 0,不再继续。
解法2:
一种数学证明过程。

代码
class Solution {
public:
string printBin(double num) {
string res = "0.";
while(res.size() < 32 && num){
num *= 2;
if (num < 1)
res += "0";
else {
res += "1";
--num;
}
}
return num ? "ERROR" : res;
}
};2023.3.3
1487.保证文件名唯一
题干
给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹:在第 i 分钟,新建名为 names[i] 的文件夹。
由于两个文件不能共享相同的文件名,因此如果新建文件夹使用的文件名已经被占用,系统会以 (k) 的形式为新文件夹的文件名添加后缀,其中 k 是能保证文件名唯一的 最小正整数 。
返回长度为 n 的字符串数组,其中 ans[i] 是创建第 i 个文件夹时系统分配给该文件夹的实际名称。
示例
示例 1:
输入:names = ["gta","gta(1)","gta","avalon"]
输出:["gta","gta(1)","gta(2)","avalon"]示例 2:
输入:names = ["wano","wano","wano","wano"]
输出:["wano","wano(1)","wano(2)","wano(3)"]示例 3:
输入:names = ["kaido","kaido(1)","kaido","kaido(1)"]
输出:["kaido","kaido(1)","kaido(2)","kaido(1)(1)"]
解释:注意,如果含后缀文件名被占用,那么系统也会按规则在名称后添加新的后缀 (k) 。解法
基本思路:
看到 “ 唯一 ” ,马上就想到了哈希表。key为实际文件名,value记录当前文件名加上后缀时当前存在的最大值。
直接使用输入的names,用哈希表判断是否有重名,只对重名的元素进行修改并记录在哈希表中,节约空间。
执行用时只击败了18%用户,,,不知时间上还可以怎么缩减。
代码
class Solution {
public:
vector<string> getFolderNames(vector<string>& names) {
unordered_map<string, int> hash;
for(int i = 0; i < names.size(); ++i){
if(hash[names[i]]){
int cnt = hash[names[i]] - 1;
while(hash[names[i] + "(" + to_string(++cnt) + ")"]);
hash[names[i]] = cnt;
names[i] += "(" + to_string(cnt) + ")";
}
hash[names[i]] = 1;
}
return names;
}
};1967.作为子字符串出现在单词中的字符串数目
题干
给你一个字符串数组 patterns 和一个字符串 word ,统计 patterns 中有多少个字符串是 word 的子字符串。返回字符串数目。
子字符串 是字符串中的一个连续字符序列。
示例
示例 1:
输入:patterns = ["a","abc","bc","d"], word = "abc"
输出:3示例 2:
输入:patterns = ["a","b","c"], word = "aaaaabbbbb"
输出:2示例 3:
输入:patterns = ["a","a","a"], word = "ab"
输出:3解法
一开始看到字符串匹配,第一反应就是经典的KMP算法。(印象深刻,考研那会儿在k = next[k];上卡了好久hhh)
然而在实际场景中,需要匹配的字符串都是较短且无序随机的,初始化的时间开销、额外的空间开销反而会更消耗资源,在字符串搜索中并不实用。因此提交代码后发现执行用时和内存消耗都不低。
查询了一下,在例如Java的String.indexOf中,使用的是暴力方法进行字符串匹配。在glibc中的strstr函数,则采用的是Two-Way算法。
这些库函数均未使用KMP算法,原因在于:
- KMP需要对字符串预处理,这个需要花时间,如果做多次查找的话,这部分预处理的时间可以分摊到多次查找里面,平摊后时间较短,但是如果只做一次查找,这部分时间是不能忽略的。
- KMP的核心思想是跳跃遍历(而不是逐个字节遍历)但是跳跃遍历破坏了CPU对内存的预取且不能进行SIMD优化。
代码
class Solution {
public:
vector<int> getNextArr(string p){
vector<int> next(p.length());
next[0] = -1;
int k = -1, j = 0;
while(j < p.length() - 1){
if(k == -1 || p[j] == p[k])
next[++j] = ++k;
else
k = next[k];
}
return next;
}
int kmp(string pattern, string word){
int i = 0, j = 0;
int pLen = pattern.length(), wLen = word.length();
vector<int> next = getNextArr(pattern);
while(i < wLen && j < pLen){
if(j == -1 || word[i] == pattern[j]){
++i;
++j;
}
else{
j = next[j];
}
}
return j == pattern.length() ? 1 : 0;
}
int numOfStrings(vector<string>& patterns, string word) {
int cnt = 0;
for(int i = 0; i < patterns.size(); ++i)
cnt += kmp(patterns[i], word);
return cnt;
}
};2023.3.5
1599.经营摩天轮的最大利润
题干
你正在经营一座摩天轮,该摩天轮共有 4 个座舱 ,每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱,但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。
给你一个长度为 n 的数组 customers , customers[i] 是在第 i 次轮转(下标从 0 开始)之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ,一旦该座舱再次抵达地面,他们就会离开座舱结束游玩。
你可以随时停下摩天轮,即便是 在服务所有游客之前 。如果你决定停止运营摩天轮,为了保证所有游客安全着陆,将免费进行所有后续轮转 。注意,如果有超过 4 位游客在等摩天轮,那么只有 4 位游客可以登上摩天轮,其余的需要等待 下一次轮转 。
返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案,则返回 -1 。
示例
示例 1:
输入:customers = [8,3], boardingCost = 5, runningCost = 6
输出:3
解释:座舱上标注的数字是该座舱的当前游客数。
1. 8 位游客抵达,4 位登舱,4 位等待下一舱,摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。
2. 3 位游客抵达,4 位在等待的游客登舱,其他 3 位等待,摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。
3. 最后 3 位游客登舱,摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。
轮转 3 次得到最大利润,最大利润为 $37 。示例 2:
输入:customers = [10,9,6], boardingCost = 6, runningCost = 4
输出:7
解释:
1. 10 位游客抵达,4 位登舱,6 位等待下一舱,摩天轮轮转。当前利润为 4 * $6 - 1 * $4 = $20 。
2. 9 位游客抵达,4 位登舱,11 位等待(2 位是先前就在等待的,9 位新加入等待的),摩天轮轮转。当前利润为 8 * $6 - 2 * $4 = $40 。
3. 最后 6 位游客抵达,4 位登舱,13 位等待,摩天轮轮转。当前利润为 12 * $6 - 3 * $4 = $60 。
4. 4 位登舱,9 位等待,摩天轮轮转。当前利润为 * $6 - 4 * $4 = $80 。
5. 4 位登舱,5 位等待,摩天轮轮转。当前利润为 20 * $6 - 5 * $4 = $100 。
6. 4 位登舱,1 位等待,摩天轮轮转。当前利润为 24 * $6 - 6 * $4 = $120 。
7. 1 位登舱,摩天轮轮转。当前利润为 25 * $6 - 7 * $4 = $122 。
轮转 7 次得到最大利润,最大利润为$122 。示例 3:
输入:customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
输出:-1
解释:
1. 3 位游客抵达,3 位登舱,0 位等待,摩天轮轮转。当前利润为 3 * $1 - 1 * $92 = -$89 。
2. 4 位游客抵达,4 位登舱,0 位等待,摩天轮轮转。当前利润为 is 7 * $1 - 2 * $92 = -$177 。
3. 0 位游客抵达,0 位登舱,0 位等待,摩天轮轮转。当前利润为 7 * $1 - 3 * $92 = -$269 。
4. 5 位游客抵达,4 位登舱,1 位等待,摩天轮轮转。当前利润为 12 * $1 - 4 * $92 = -$356 。
5. 1 位游客抵达,2 位登舱,0 位等待,摩天轮轮转。当前利润为 13 * $1 - 5 * $92 = -$447 。
利润永不为正,所以返回 -1 。解法
基本思路:
最开始直接排除掉哪怕坐满(4个游客)都不盈利的情况。
之后一遍for循环肯定是要的,得到在没有新游客来时,轮转的最大收益及所在轮次。
这时计算出每次轮转盈利时需要的最小游客数。
对剩下排队的人数进行判断,如果剩下的人数超过了最小值,则按照4个一轮的最大收益方案计算,一定为最大收益。轮次数加上剩余人数 / 4的商,若余数依旧大于最小值,再加一。
需要注意的是,存在之前for循环中前面的轮次的盈利额与后面轮次的盈利额相同时不更新轮次数的情况,因此有多余人数的情况下,需要先更新轮次数至n。
(总感觉逻辑有哪里不完善。。)
代码
class Solution {
public:
int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {
if(4 * boardingCost - runningCost <= 0) return -1;
int curP = 0, leftP = 0, curVal = 0, maxVal = 0;
int turns = -1;
for(int i = 0; i < customers.size(); ++i){
leftP += customers[i];
curP = min(4, leftP);
curVal += curP * boardingCost - runningCost;
leftP -= curP;
if(curVal > maxVal){
turns = i + 1;
maxVal = curVal;
}
}
int minP = runningCost / boardingCost + 1;
if (leftP >= minP){
if(turns < customers.size())
turns = customers.size();
turns += leftP / 4 + (leftP % 4 >= minP ? 1 : 0);
}
return turns;
}
};2023.3.6
1653.使字符串平衡的最少删除次数
题干
给你一个字符串 s ,它仅包含字符 ‘a’ 和 ‘b’ 。
你可以删除 s 中任意数目的字符,使得 s 平衡 。当不存在下标对 (i,j) 满足 i < j ,且 s[i] = ‘b’ 的同时 s[j]= ‘a’ ,此时认为 s 是 平衡 的。
请你返回使 s 平衡 的 最少 删除次数。
示例
示例 1:
输入:s = "aababbab"
输出:2
解释:你可以选择以下任意一种方案:
下标从 0 开始,删除第 2 和第 6 个字符("aababbab" -> "aaabbb"),
下标从 0 开始,删除第 3 和第 6 个字符("aababbab" -> "aabbbb")。示例 2:
输入:s = "bbaaaaabb"
输出:2
解释:唯一的最优解是删除最前面两个字符。解法
基本思路:
存在这么一条分割线,使得通过最少次改动让线左边的字母全是a,右边全是b。
那么把s中每个字符后的位置分别作为分割线,计算需要修改的值,记录其中最小的即可。
如果再对分割线左右进行遍历,双重循环比较浪费时间,可以采用前缀和的方式。
先记录整个 s 中 a 的个数,分割线共有 s.length + 1 个位置,在 s[0] 左边时,意味着整个s中的a都需要修改,把a的个数作为修改次数。
此后分割线每往右移动一格,判断移动时跨过的字符是否为a,如果为a,需要将之前统计的次数 -1 ,若为b,则还需要再 + 1 。
最后返回每个位置中的最小值即可。
代码
class Solution {
public:
int minimumDeletions(string s) {
int cnt = 0;
for(int i = 0; i < s.length(); ++i)
cnt += 'b' - s[i];
int res = cnt;
for(int i = 0; i < s.length(); ++i){
cnt -= 'b' - s[i] ? 1 : -1;
res = min(res, cnt);
}
return res;
}
};优化
动态规划
将问题拆分,考虑s的最后一个字符:
- 为 b ,无需删除,问题规模缩小为:使 s 的前 n − 1 个字符平衡的最少删除次数;
- 为 a ,两种情况,1.删除,问题规模缩小为: 使 s 的前 n − 1 个字符平衡的最少删除次数 + 1;2.保留,需要删除前面的所有 b 。选择其中次数最少的。
定义一个 f[i] 表示:使 s 的前 i 个字符平衡的最少删除次数,可以得到:
- 为 b ,f[i] = f[i - 1];
- 为 a ,min(f[i - 1] + 1, b的数量)
最终答案为 f[n] 。
推理这个公式时,实际是上述思路的逆过程,拆分时从后开始由大到小,计算时从前开始由小到大。
class Solution {
public:
int minimumDeletions(string s) {
int f = 0, cnt_b = 0;
for (char c : s)
if (c == 'b') ++cnt_b;
else f = min(f + 1, cnt_b);
return f;
}
};2023.3.7
1422.分割字符串的最大得分
题干
给你一个由若干 0 和 1 组成的字符串 s ,请你计算并返回将该字符串分割成两个 非空 子字符串(即 左 子字符串和 右 子字符串)所能获得的最大得分。
「分割字符串的得分」为 左 子字符串中 0 的数量加上 右 子字符串中 1 的数量。
示例
示例 1:
输入:s = "011101"
输出:5 示例 2:
输入:s = "1111"
输出:3解法
基本思路:
和昨天那题一模一样的思路。
代码
class Solution {
public:
int maxScore(string s) {
int cnt1 = 0;
for(int i = 0; i < s.length(); ++i){
cnt1 += s[i] - '0';
}
int maxVal = 0;
for(int i = 0; i < s.length() - 1; ++i){
cnt1 += s[i] - '0' ? -1 : 1;
maxVal = max(maxVal, cnt1);
}
return maxVal;
}
};2023.3.8
剑指offer47.礼物的最大价值
题干
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物解法
基本思路:
从其中一格到它的右下角只有两种拿法,往下往右或者往右往下,取决于两个里选哪个。第一反应就是动态规划。
如示例1,22处的最大值取决于11的最大值加上12和21中的最大值 ——> 11的最大值取决于00的最大值加上01和10中的最大值.
设 res{i}{j} 为该处的最大值,则有 res{i}{j} = max(res{i - 1}{j},res{i}{j - 1}) + grid{i - 1}{j - 1}, 结果为res{m}{n}
代码
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> res(m+1, vector<int>(n+1));
for(int i = 1; i <= m; ++i){
for(int j = 1; j <= n; ++j){
res[i][j] = max(res[i - 1][j], res[i][j - 1]) + grid[i - 1][j - 1];
}
}
return res[m][n];
}
};剑指offer Ⅱ 060.出现频率最高的k个数字
题干
给定一个整数数组 nums 和一个整数 k ,请返回其中出现频率前 k 高的元素。可以按 任意顺序 返回答案。
进阶:所设计算法的时间复杂度 必须 优于 O(n log n) ,其中 n 是数组大小。
示例
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]示例 2:
输入: nums = [1], k = 1
输出: [1]解法
基本思路:
第一遍for循环遍历,用哈希表存储每个数字出现的次数。
使用优先队列(底层是堆实现),自定义比较方式为从小到大(小根堆),这样堆顶元素是最小的,便于排除。
第二遍for循环将前k个数字出现的次数加入队列,之后的数字若出现次数更多,替换堆顶元素。
代码
class Solution {
public:
struct cmp {
bool operator()(pair<int,int> &m,pair<int,int> &n) {
return m.second>n.second;
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> cnt;
for(int i = 0; i < nums.size(); ++i){
cnt[nums[i]]++;
}
priority_queue<pair<int,int>,vector<pair<int,int>>,cmp> q;
for(auto x : cnt){
if(q.size() == k){
if(x.second > q.top().second){
q.pop();
q.push(x);
}
}
else
q.push(x);
}
vector<int> res;
while(!q.empty()){
res.push_back(q.top().first);
q.pop();
}
return res;
}
};2023.3.9
2379.得到K个黑块的最少涂色次数
题干
给你一个长度为 n 下标从 0 开始的字符串 blocks ,blocks[i] 要么是 ‘W‘ 要么是 ‘B‘ ,表示第 i 块的颜色。字符 ‘W‘ 和 ‘B‘ 分别表示白色和黑色。
给你一个整数 k ,表示想要 连续 黑色块的数目。每一次操作中,你可以选择一个白色块将它 涂成 黑色块。
请你返回至少出现 一次 连续 k 个黑色块的 最少 操作次数。
示例
示例 1:
输入:blocks = "WBBWWBBWBW", k = 7
输出:3
解释:一种得到 7 个连续黑色块的方法是把第 0 ,3 和 4 个块涂成黑色。得到 blocks = "BBBBBBBWBW" 。
可以证明无法用少于 3 次操作得到 7 个连续的黑块。所以我们返回 3 。示例 2:
输入:blocks = "WBWBBBW", k = 2
输出:0
解释:不需要任何操作,因为已经有 2 个连续的黑块。所以我们返回 0 。解法
基本思路:
把白色变成黑色的最少操作次数,其实就是求长为k的滑动窗口内白色的数量。
维护双指针增减白色的数量,取最小值即可。
代码
class Solution {
public:
int minimumRecolors(string blocks, int k) {
int cnt = 0;
for(int i = 0; i < k; ++i){
if(blocks[i] - 'B')
++cnt;
}
int res = cnt;
for(int i = k; i < blocks.length(); ++i){
if(blocks[i] - 'B')
++cnt;
if(blocks[i - k] - 'B')
--cnt;
res = min(res, cnt);
}
return res;
}
};1753.移除石子的最大得分
题干
你正在玩一个单人游戏,面前放置着大小分别为 a、b 和 c 的 三堆 石子。
每回合你都要从两个 不同的非空堆 中取出一颗石子,并在得分上加 1 分。当存在 两个或更多 的空堆时,游戏停止。
给你三个整数 a 、b 和 c ,返回可以得到的 最大分数 。
示例
示例 1:
输入:a = 2, b = 4, c = 6
输出:6
解释:石子起始状态是 (2, 4, 6) ,最优的一组操作是:
- 从第一和第三堆取,石子状态现在是 (1, 4, 5)
- 从第一和第三堆取,石子状态现在是 (0, 4, 4)
- 从第二和第三堆取,石子状态现在是 (0, 3, 3)
- 从第二和第三堆取,石子状态现在是 (0, 2, 2)
- 从第二和第三堆取,石子状态现在是 (0, 1, 1)
- 从第二和第三堆取,石子状态现在是 (0, 0, 0)
总分:6 分 。示例 2:
输入:a = 4, b = 4, c = 6
输出:7解法
基本思路:
同2335.
代码
class Solution {
public:
int maximumScore(int a, int b, int c) {
int res = 0;
vector<int> arr = {a, b, c};
sort(arr.begin(), arr.end());
while(arr[1] != 0){
arr[1]--;
arr[2]--;
res++;
sort(arr.begin(), arr.end());
}
return res;
}
};优化

class Solution {
public:
int maximumScore(int a, int b, int c) {
int d = max(max(a, b), c), ab = a + b + c - d;
return ab < d ? ab : (a + b + c) / 2;
}
};2023.3.10
1590.使数组和能被P整除
题干
给你一个正整数数组 nums,请你移除 最短 子数组(可以为 空),使得剩余元素的 和 能被 p 整除。 不允许 将整个数组都移除。
请你返回你需要移除的最短子数组的长度,如果无法满足题目要求,返回 -1 。
子数组 定义为原数组中连续的一组元素。
示例
示例 1:
输入:nums = [3,1,4,2], p = 6
输出:1
解释:nums 中元素和为 10,不能被 p 整除。我们可以移除子数组 [4] ,剩余元素的和为 6 。示例 2:
输入:nums = [1,2,3], p = 3
输出:0示例 3:
输入:nums = [1,2,3], p = 7
输出:-1解法
基本思路:
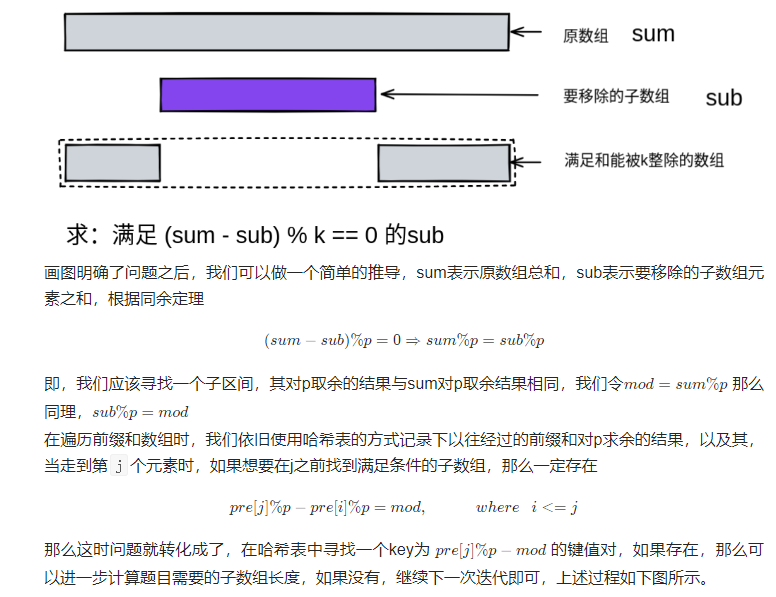
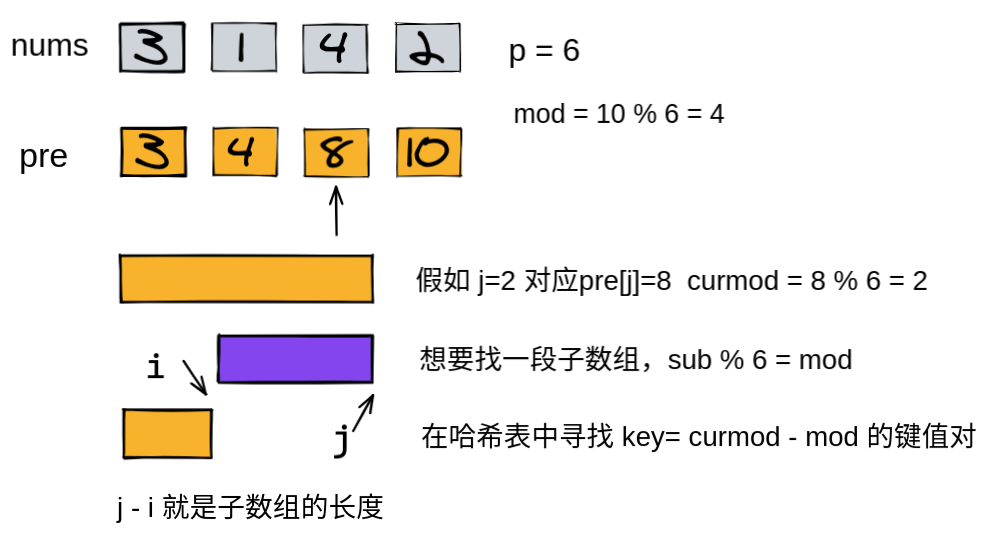
**tips1: ** 哨兵思想的应用,处理当前缀和求余等于0时的情况,此时 i 作为下标,表示的位置为第 i + 1 个,因此设为-1。
tips2: 存在前缀和的余数小于总和余数的情况,因此需要 + p ,保证为正数。
tips3: 一开始用的 if(hash[target]) 进行判断,调试时发现这样会产生 hash[target] = 0 的初始化操作,影响后续判断计算,因此改用成员函数count。
代码
class Solution {
public:
int minSubarray(vector<int>& nums, int p) {
int mod = 0;
for(int i = 0; i < nums.size(); ++i)
mod = (mod + nums[i]) % p;
if(mod == 0)
return 0;
int cur = 0, target = 0, res = nums.size();
unordered_map<int, int> hash;
// tips1
hash[0] = -1;
for(int i = 0; i < nums.size(); ++i){
cur = (cur + nums[i]) % p;
// tips2
target = (cur - mod + p) % p;
// tips3
if(hash.count(target))
res = min(res, i - hash[target]);
hash[cur] = i;
}
return res == nums.size() ? -1 : res;
}
};2023.3.13
2383.赢得比赛需要的最少训练时长
题干
你正在参加一场比赛,给你两个 正 整数 initialEnergy 和 initialExperience 分别表示你的初始精力和初始经验。
另给你两个下标从 0 开始的整数数组 energy 和 experience,长度均为 n 。
你将会 依次 对上 n 个对手。第 i 个对手的精力和经验分别用 energy[i] 和 experience[i] 表示。当你对上对手时,需要在经验和精力上都 严格 超过对手才能击败他们,然后在可能的情况下继续对上下一个对手。
击败第 i 个对手会使你的经验 增加 experience[i],但会将你的精力 减少 energy[i] 。
在开始比赛前,你可以训练几个小时。每训练一个小时,你可以选择将增加经验增加 1 或者 将精力增加 1 。
返回击败全部 n 个对手需要训练的 最少 小时数目。
示例
示例 1:
输入:initialEnergy = 5, initialExperience = 3, energy = [1,4,3,2], experience = [2,6,3,1]
输出:8示例 2:
输入:initialEnergy = 2, initialExperience = 4, energy = [1], experience = [3]
输出:0解法
基本思路:
自身的精力要加到比energy数组的和多1,自身的经验只要每次比当前比较的数多1即可。
代码
class Solution {
public:
int minNumberOfHours(int initialEnergy, int initialExperience, vector<int>& energy, vector<int>& experience) {
int sumE = 0, addEx, minH;
for(int i = 0; i < energy.size(); ++i)
sumE += energy[i];
minH = sumE < initialEnergy ? 0 : sumE - initialEnergy + 1;
for(int i = 0; i < experience.size(); ++i){
addEx = initialExperience > experience[i] ? 0 : experience[i] - initialExperience + 1;
minH += addEx;
initialExperience += experience[i] + addEx;
}
return minH;
}
};2023.3.14
1605.给定行和列的和求可行矩阵
题干
给你两个非负整数数组 rowSum 和 colSum ,其中 rowSum[i] 是二维矩阵中第 i 行元素的和, colSum[j] 是第 j 列元素的和。换言之你不知道矩阵里的每个元素,但是你知道每一行和每一列的和。
请找到大小为 rowSum.length x colSum.length 的任意 非负整数 矩阵,且该矩阵满足 rowSum 和 colSum 的要求。
请你返回任意一个满足题目要求的二维矩阵,题目保证存在 至少一个 可行矩阵。
示例
示例 1:
输入:rowSum = [3,8], colSum = [4,7]
输出:[[3,0],
[1,7]]示例 2:
输入:rowSum = [5,7,10], colSum = [8,6,8]
输出:[[0,5,0],
[6,1,0],
[2,0,8]]示例 3:
输入:rowSum = [0], colSum = [0]
输出:[[0]]解法
基本思路:
由于保证存在解,直接用贪心即可。
代码
class Solution {
public:
vector<vector<int>> restoreMatrix(vector<int>& rowSum, vector<int>& colSum) {
int row = rowSum.size(), col = colSum.size();
vector<vector<int>> res(row, vector<int>(col));
for(int i = 0; i < row; ++i){
for(int j = 0; j < col; ++j){
res[i][j] = min(rowSum[i], colSum[j]);
rowSum[i] -= res[i][j];
colSum[j] -= res[i][j];
}
}
return res;
}
};2023.3.15
1615.最大网络秩
题干
n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。
两座不同城市构成的 城市对 的 网络秩 定义为:与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市,则这条道路只计算 一次 。
整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。给你整数 n 和数组 roads,返回整个基础设施网络的 最大网络秩 。
示例
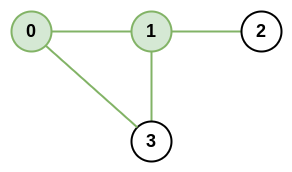
示例 1:
输入:n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出:4
解释:城市 0 和 1 的网络秩是 4,因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。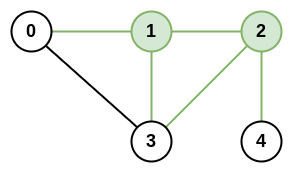
示例 2:
输入:n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
输出:5
解释:共有 5 条道路与城市 1 或 2 相连。示例 3:
输入:n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
输出:5
解释:2 和 5 的网络秩为 5,注意并非所有的城市都需要连接起来。解法
基本思路:
暴力解法。统计与每个城市相连的道路数cnt,统计每对城市间是否存在道路,可计算得城市对a、b的最大网络秩为 **cnt[a] + cnt[b] - connected[a] [b]**。
遍历所有不重复的城市对即可。
代码
class Solution {
public:
int maximalNetworkRank(int n, vector<vector<int>>& roads) {
vector<int> cnt(n);
vector<vector<int>> connected(n, vector<int>(n));
for(auto pair : roads){
cnt[pair[0]]++;
cnt[pair[1]]++;
connected[pair[0]][pair[1]] = 1;
connected[pair[1]][pair[0]] = 1;
}
int maxRank = 0, rank;
for(int i = 0; i < n ; ++i){
for(int j = i + 1; j < n ; ++j){
rank = cnt[i] + cnt[j] - connected[i][j];
maxRank = max(maxRank, rank);
}
}
return maxRank;
}
};441.排列硬币
题干
你总共有 n 枚硬币,并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯,其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。
给你一个数字 n ,计算并返回可形成 完整阶梯行 的总行数。
示例
示例 1:
输入:n = 5
输出:2示例 2:
输入:n = 8
输出:3解法
- 解方程
- 二分查找
代码
1.因为n取值很大,乘以常数后可能超出int取值范围,因此需转化为long long型。
class Solution {
public:
int arrangeCoins(int n) {
return static_cast<int>((sqrt(8 * (long long)n + 1) - 1) / 2);
}
};2.一开始使用了暴力for循环,太慢了,就想到了二分进行优化。
class Solution {
public:
int arrangeCoins(int n) {
int l = 1, r = n;
while(l < r){
int mid = l + (r - l + 1) / 2;
if((long long)mid * (mid + 1) <= (long long)2 * n)
l = mid;
else
r = mid - 1;
}
return l;
}
};LCP 02.分式简化
题干
有一个同学在学习分式。他需要将一个连分数化成最简分数,你能帮助他吗?
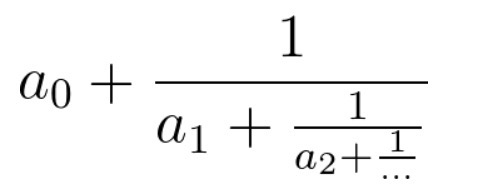
连分数是形如上图的分式。在本题中,所有系数都是大于等于0的整数。
输入的cont代表连分数的系数(cont[0]代表上图的a0,以此类推)。返回一个长度为2的数组**[n, m],使得连分数的值等于n / m,且n, m最大公约数为1**。
示例
示例 1:
输入:cont = [3, 2, 0, 2]
输出:[13, 4]
解释:原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。示例 2:
输入:cont = [0, 0, 3]
输出:[3, 1]
解释:如果答案是整数,令分母为1即可。解法
数学

代码
class Solution {
public:
vector<int> fraction(vector<int>& cont) {
int m = 1, n = 0;
for(int i = cont.size() - 1; i > 0; --i){
int temp = m;
m = cont[i] * m + n;
n = temp;
}
return {cont[0] * m + n, m};
}
};2023.3.17
2389.和有限的最长子序列
题干
给你一个长度为 n 的整数数组 nums ,和一个长度为 m 的整数数组 queries 。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是 nums 中 元素之和 小于等于 queries[i] 的 子序列 的 最大 长度 。
子序列 是由一个数组删除某些元素(也可以不删除)但不改变剩余元素顺序得到的一个数组。
示例
示例 1:
输入:nums = [4,5,2,1], queries = [3,10,21]
输出:[2,3,4]示例 2:
输入:nums = [2,3,4,5], queries = [1]
输出:[0]解法
基本思路:
先给nums排个序,然后for循环比较queries每个元素最大比前几个nums的元素和大就行。
自己的方法是直接暴力求和一个个比较过去;
题解采用了前缀和统计+二分查找的方法来优化比较的起始位置,但是实际提交发现在给定的测试用例中好像并没有比暴力快。
哦,我就看了个标题,代码里用的 upper_bound() 库函数,难怪比我自己实现的快。
代码
class Solution {
public:
// 我的方案
vector<int> answerQueries(vector<int>& nums, vector<int>& queries) {
sort(nums.begin(), nums.end());
for(int i = 0; i < queries.size(); ++i){
int sum = 0, cnt = 0;
while(queries[i] >= sum && cnt < nums.size())
sum += nums[cnt++];
if(sum > queries[i])
cnt--;
queries[i] = cnt;
}
return queries;
}
};
class Solution {
public:
// 题解方法:前缀和+二分查找
int binarySearch(vector<int>& nums, int num){
int l = 0, r = nums.size() - 1;
while(l < r){
int mid = (r - l + 1) / 2 + l;
if (nums[mid] <= num)
l = mid;
else
r = mid - 1;
}
return l;
}
vector<int> answerQueries(vector<int>& nums, vector<int>& queries) {
vector<int> sums(nums.size());
sort(nums.begin(), nums.end());
sums[0] = nums[0];
for(int i = 1; i < nums.size(); ++i){
sums[i] = nums[i] + sums[i - 1];
}
for(int i = 0; i < queries.size(); ++i){
int idx = binarySearch(nums, queries[i]);
while(queries[i] < sums[idx] && idx >= 0){
if(--idx < 0)
break;
}
queries[i] = idx + 1;
}
return queries;
}
};1254.统计封闭岛屿的数目
题干
二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。
请返回 封闭岛屿 的数目。
示例
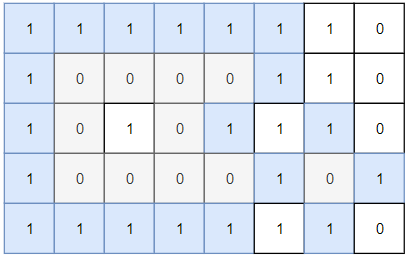
示例 1:
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出:2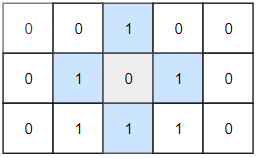
示例 2:
输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出:1解法
基本思路:
可以发现封闭岛屿必然不会出现在矩阵的边缘,因为需要被1全包裹。
也就是说可以先统计全部的岛屿数量,然后去除在边缘的岛屿就是答案。
可以用DFS,向四个方向搜索来找到一个连通域(想到了图像处理里的找连通域,简化版)。但是不方便在DFS函数中去统计总数,所以想到了标记(覆盖 / 污染)。
DFS的作用为标记一整个连通域为1.
那么只要先把边缘的连通域都标记为1,之后剩下的连通域每标记一个,就cnt++就行。
代码
class Solution {
public:
void dfs(vector<vector<int>>& grid, int x, int y){
int m = grid.size(), n = grid[0].size();
if(x < 0 || x >= m || y < 0 || y >= n)
return;
if(grid[x][y])
return;
grid[x][y] = 2;
dfs(grid, x, y + 1);
dfs(grid, x + 1, y);
dfs(grid, x, y - 1);
dfs(grid, x - 1, y);
}
int closedIsland(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
for(int i = 0; i < m; ++i){
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
for(int i = 0; i < n; ++i){
dfs(grid, 0, i);
dfs(grid, m - 1, i);
}
int cnt = 0;
for(int i = 0; i < m; ++i){
for(int j = 0; j < n; ++j){
if(!grid[i][j]){
cnt++;
dfs(grid, i, j);
}
}
}
return cnt;
}
};2023.3.18
1616.分割两个字符串得到回文串
题干
给你两个字符串 a 和 b ,它们长度相同。请你选择一个下标,将两个字符串都在 相同的下标 分割开。由 a 可以得到两个字符串: aprefix 和 asuffix ,满足 a = aprefix + asuffix ,同理,由 b 可以得到两个字符串 bprefix 和 bsuffix ,满足 b = bprefix + bsuffix 。请你判断 aprefix + bsuffix 或者 bprefix + asuffix 能否构成回文串。
当你将一个字符串 s 分割成 sprefix 和 ssuffix 时, ssuffix 或者 sprefix 可以为空。比方说, s = “abc” 那么 “” + “abc” , “a” + “bc” , “ab” + “c” 和 “abc” + “” 都是合法分割。如果 能构成回文字符串 ,那么请返回 true,否则返回 false 。
注意, x + y 表示连接字符串 x 和 y 。
示例
示例 1:
输入:a = "x", b = "y"
输出:true示例 2:
输入:a = "abdef", b = "fecab"
输出:true解法
基本思路:
双指针。
回文串其实是分为两部分对应的。第一部分是a的头和b的尾(可能为空),第二部分是ab任一的中部(也可能为空)。
那么只需要维护两个指针,分别从a头b尾向中间扫描对比,遇到不同的字符就跳转到第二部分,a和b中间部分(区间 [l, r])若是回文串,则返回ture。否则再从b头a尾开始重复一遍。
写法可能有点问题,和一个题解思路相同但是速度慢了一些。
代码
class Solution {
public:
bool isPalindrome(string s, int l, int r){
while(s[l] == s[r]){
if(r - l > 2){
l++;
r--;
}
else
return true;
}
return false;
}
bool checkPalindromeFormation(string a, string b) {
int l = 0, r = b.length() - 1;
while(a[l] == b[r]){
if(r - l > 2){
l++;
r--;
}
else
return true;
}
if(isPalindrome(a, l, r) || isPalindrome(b, l, r))
return true;
l = 0;
r = a.length() - 1;
while(b[l] == a[r]){
if(r - l > 2){
l++;
r--;
}
else
return true;
}
if(isPalindrome(b, l, r) || isPalindrome(a, l, r))
return true;
return false;
}
};2032.至少在两个数组中出现的值
题干
给你三个整数数组 nums1、nums2 和 nums3 ,请你构造并返回一个 元素各不相同的 数组,且由 至少 在 两个 数组中出现的所有值组成。数组中的元素可以按 任意 顺序排列。
示例
示例 1:
输入:nums1 = [1,1,3,2], nums2 = [2,3], nums3 = [3]
输出:[3,2]示例 2:
输入:nums1 = [1,2,2], nums2 = [4,3,3], nums3 = [5]
输出:[]解法
基本思路:枚举。
代码
class Solution {
public:
vector<int> twoOutOfThree(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3) {
vector<int> res;
int cnt1[101] = {0};
int cnt2[101] = {0};
int cnt3[101] = {0};
for(auto x : nums1)
cnt1[x] = 1;
for(auto x : nums2)
cnt2[x] = 1;
for(auto x : nums3)
cnt3[x] = 1;
for(int i = 1; i < 101; ++i){
if(cnt1[i] + cnt2[i] + cnt3[i] > 1)
res.push_back(i);
}
return res;
}
};1984.学生分数的最小差值
题干
给你一个 下标从 0 开始 的整数数组 nums ,其中 nums[i] 表示第 i 名学生的分数。另给你一个整数 k 。
从数组中选出任意 k 名学生的分数,使这 k 个分数间 最高分 和 最低分 的 差值 达到 最小化 。
返回可能的 最小差值 。
示例
示例 1:
输入:nums = [90], k = 1
输出:0示例 2:
输入:nums = [9,4,1,7], k = 2
输出:2解法
基本思路:
先给nums排序,然后遍历找长度为k的子数组的最大差值中的最小值。
代码
class Solution {
public:
int minimumDifference(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
int minSub = nums.back() - nums[0];
for(int i = 0; i < nums.size() - k + 1; ++i)
minSub = min(minSub, nums[i + k - 1] - nums[i]);
return minSub;
}
};2465.不同的平均值数目
题干
给你一个下标从 0 开始长度为 偶数 的整数数组 nums 。
只要 nums 不是 空数组,你就重复执行以下步骤:
找到 nums 中的最小值,并删除它。
找到 nums 中的最大值,并删除它。
计算删除两数的平均值。
比方说,2 和 3 的平均值是 (2 + 3) / 2 = 2.5 。返回上述过程能得到的 不同 平均值的数目。
注意 ,如果最小值或者最大值有重复元素,可以删除任意一个。
示例
示例 1:
输入:nums = [4,1,4,0,3,5]
输出:2示例 2:
输入:nums = [1,100]
输出:1解法
基本思路:
先给nums排序,然后双指针每次分别从头尾各取一个值计算平均值加入哈希表,最后返回哈希表中的键值对数。
代码
class Solution {
public:
int distinctAverages(vector<int>& nums) {
unordered_map<double, int> res;
sort(nums.begin(), nums.end());
for(int i = 0, j = nums.size() - 1; i < nums.size() / 2; ++i, --j)
res[(nums[i] + nums[j]) / 2.0] = 1;
return res.size();
}
};8.字符串转换整数
题干
实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。
注意:
本题中的空白字符只包括空格字符 ‘ ‘ 。
除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例
示例 1:
输入:s = "42"
输出:42示例 2:
输入:s = " -42"
输出:-42示例 3:
输入:s = "4193 with words"
输出:4193解法
基本思路:
简单的if判断。
- 结果可能超出int,因此用long long存储;
- 用sign为1 或 -1表示符号位方便计算;
- 宏定义 INT_MAX 和 INT_MIN 。
代码
class Solution {
public:
int myAtoi(string s) {
int sign = 1;
bool isPre = true;
long long res = 0;
for(auto x : s){
if(isPre){
if(x == ' ') continue;
else if(x == '+') isPre = false;
else if(x == '-'){
isPre = false;
sign = -1;
}
else if(x >= '0' && x <= '9'){
isPre = false;
res = x - '0';
}
else
return 0;
}
else{
if(x >= '0' && x <= '9'){
res = res * 10 + x - '0';
if(res * sign > INT_MAX)
return INT_MAX;
if(res * sign < INT_MIN)
return INT_MIN;
}
else
return res * sign;
}
}
return res * sign;
}
};2023.3.21
2469.温度转换
题干
给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度,以 摄氏度(Celsius)为单位。
你需要将摄氏度转换为 开氏度(Kelvin)和 华氏度(Fahrenheit),并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。
返回数组 ans 。与实际答案误差不超过 10e-5 的会视为正确答案。
- 开氏度 = 摄氏度 + 273.15
- 华氏度 = 摄氏度 * 1.80 + 32.00
示例
示例 1:
输入:celsius = 36.50
输出:[309.65000,97.70000]示例 2:
输入:celsius = 122.11
输出:[395.26000,251.79800]解法
基本思路:。。。
代码
class Solution {
public:
vector<double> convertTemperature(double celsius) {
return {celsius + 273.15, celsius * 1.8 + 32};
}
};2023.3.26
2395.和相等的子数组
题干
给你一个下标从 0 开始的整数数组 nums ,判断是否存在 两个 长度为 2 的子数组且它们的 和 相等。注意,这两个子数组起始位置的下标不相同 。如果这样的子数组存在,请返回 true,否则返回 false 。
子数组 是一个数组中一段连续非空的元素组成的序列。
示例
示例 1:
输入:nums = [4,2,4]
输出:true示例 2:
输入:nums = [0,0,0]
输出:true解法
基本思路:哈希表的唯一性作为判断依据。
代码
class Solution {
public:
bool findSubarrays(vector<int>& nums) {
unordered_set<int> sums;
for(int i = 1; i < nums.size(); ++i){
int sum = nums[i-1] + nums[i];
if(sums.count(sum))
return true;
sums.emplace(sum);
}
return false;
}
};215.数组中的第K个最大元素
题干
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4解法
基本思路:
要求时间复杂度为 O(n) 。快排和堆排的时间复杂度均为O(nlogn) ,本题实际用到了其中的一部分:快排的单趟排序和堆排的建堆,都是 O(n) 的时间复杂度。
以快排从大到小为例, 每次单趟排序把一个数放到正确的位置上。此时该位置左边的数都大于该值,右边都小于。该值所在位置和 k - 1 进行比较即可判断在该值的哪一边。然后缩小排序范围,仅在其中一边的范围内再次进行单趟排序,直至位置为 k - 1 为止。
代码
class Solution {
public:
int quickSingleSort(vector<int>& nums, int l, int r){
int pivot = l;
while(l < r){
while(l < r && nums[pivot] >= nums[r]) r--;
while(l < r && nums[pivot] <= nums[l]) l++;
if(l < r) swap(nums[l], nums[r]);
}
swap(nums[pivot], nums[l]);
return l;
}
int findKthLargest(vector<int>& nums, int k) {
int l = 0, r = nums.size() - 1;
while(1){
int idx = quickSingleSort(nums, l, r);
if(idx == k - 1)
return nums[idx];
else if(idx < k - 1)
l = idx + 1;
else
r = idx - 1;
}
}
};1588.所有奇数长度子数组的和
题干
给你一个正整数数组 arr ,请你计算所有可能的奇数长度子数组的和。
子数组 定义为原数组中的一个连续子序列。
进阶:你可以设计一个 O(n) 时间复杂度的算法解决此问题吗?
示例
示例 1:
输入:arr = [1,4,2,5,3]
输出:58示例 2:
输入:arr = [1,2]
输出:3解法
基本思路:问题转化为数学题了属于是。
转化为:统计数组中每个元素出现在所有不同子数组中的次数。
- 可以发现,在一个奇数长度子数组中,除去一个指定元素外,剩余元素数量必然为偶数,那么可以得到:该元素左右两侧的元素数量的奇偶性相同。
- 以示例1为例,1的左侧数量0,右侧数量4,那么左侧奇数可选组合为0,偶数可选组合为1(只有一个0);右侧奇数可选组合数为2(1、3),偶数可选3(0、2、4),那么1可能的所有组合数为:0 * 2 + 1 * 3 = 3。可以得到:元素总出现次数 = 左侧偶数选择 * 右侧偶数选择 + 左侧奇数选择 * 右侧奇数选择。
- 根据2中规律,只需for循环一次即可,也就是 O(n) 时间复杂度。
代码
class Solution {
public:
int sumOddLengthSubarrays(vector<int>& arr) {
int n = arr.size();
int res = 0;
for(int i = 0; i < n; ++i){
int lEven = i / 2 + 1;
int rEven = (n - i - 1) / 2 + 1;
int lOdd = (i + 1) / 2;
int rOdd = (n - i) / 2;
int num = lEven * rEven + lOdd * rOdd;
res += num * arr[i];
}
return res;
}
};2023.3.27
1638.统计只差一个字符的子串数目
题干
给你两个字符串 s 和 t ,请你找出 s 中的非空子串的数目,这些子串满足替换 一个不同字符 以后,是 t 串的子串。换言之,请你找到 s 和 t 串中 恰好 只有一个字符不同的子字符串对的数目。
比方说, “computer” and “computation” 只有一个字符不同: ‘e’/‘a’ ,所以这一对子字符串会给答案加 1 。
请你返回满足上述条件的不同子字符串对数目。
示例
示例 1:
输入:s = "aba", t = "baba"
输出:6示例 2:
输入:s = "ab", t = "bb"
输出:3解法
基本思路:枚举。
双层for循环,枚举 s 和 t 中的每个 i 、j ,当这两个字符不同时,子串的其余字符均相同。
此时对这两个字符分别向左和右扩散比较,相同则计数(l、r)+1,不同则停止。可以发现这样的不同子串有 (1 + l)*(1 + r)个。对枚举的每个字符进行这样的操作,统计总子串数即可。
代码
class Solution {
public:
int countSubstrings(string s, string t) {
int m = s.length(), n = t.length();
int res = 0;
for(int i = 0; i < m; ++i){
for(int j = 0; j < n; ++j){
if(s[i] != t[j]){
int l = 1, r = 1;
int p = i - 1, q = j - 1;
while(p >= 0 && q >= 0 && s[p--] == t[q--]) l++;
p = i + 1, q = j + 1;
while(p < m && q < n && s[p++] == t[q++]) r++;
res += l * r;
}
}
}
return res;
}
};1438.绝对差不超过限制的最长连续子数组
题干
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例
示例 1:
输入:nums = [8,2,4,7], limit = 4
输出:2 示例 2:
输入:nums = [4,2,2,2,4,4,2,2], limit = 0
输出:3解法
基本思路:双指针滑动窗口。
右指针r主动移动,左指针l被动移动(超出limit时)。需要一个数据结构来维护子数组有序(顺序容器中的map和set),由于存在重复数字,采用multiset。
注:
- begin() == rend() 均指向第一个元素,rbegin() 指向最后一个元素,end() 指向最后一个元素的下一个。
- 在multiset中,erase(elem) 擦除的是值等于elem的所有元素。
代码
class Solution {
public:
int longestSubarray(vector<int>& nums, int limit) {
multiset<int> sub;
int l = 0, r = 0;
int res = 0;
while(r < nums.size()){
sub.emplace(nums[r]);
while(*sub.rbegin() - *sub.begin() > limit)
sub.erase(sub.find(nums[l++]));
res = max(res, r - l + 1);
r++;
}
return res;
}
};424.替换后的最长重复字符
题干
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
在执行上述操作后,返回包含相同字母的最长子字符串的长度。
示例
示例 1:
输入:s = "ABAB", k = 2
输出:4示例 2:
输入:s = "AABABBA", k = 1
输出:4解法
基本思路:双指针滑动窗口。
和上题(1438)思路类似的滑动窗口双指针,统计需要修改的字符数是否超过k。因为不确定最后的子串是哪个字符,因此先将所有不同字符加入集合,全循环一遍。
代码
class Solution {
public:
int characterReplacement(string s, int k) {
unordered_set<char> letter;
for(char c : s)
letter.emplace(c);
int res = 0;
for(char c : letter){
int l = 0, r = 0;
int cnt = 0;
while(r < s.length()){
if(s[r] != c) cnt++;
while(cnt > k){
if(s[l] != c) cnt--;
l++;
}
res = max(res, r - l + 1);
r++;
}
}
return res;
}
};2023.3.28
1092.最短公共超序列(未完结)
题干
给出两个字符串 str1 和 str2,返回同时以 str1 和 str2 作为子序列的最短字符串。如果答案不止一个,则可以返回满足条件的任意一个答案。
(如果从字符串 T 中删除一些字符(也可能不删除,并且选出的这些字符可以位于 T 中的 任意位置),可以得到字符串 S,那么 S 就是 T 的子序列)
示例
示例 1:
输入:str1 = "abac", str2 = "cab"
输出:"cabac"
解释:
str1 = "abac" 是 "cabac" 的一个子串,因为我们可以删去 "cabac" 的第一个 "c"得到 "abac"。
str2 = "cab" 是 "cabac" 的一个子串,因为我们可以删去 "cabac" 末尾的 "ac" 得到 "cab"。
最终我们给出的答案是满足上述属性的最短字符串。解法
基本思路:动态规划+双指针。
我们要找的目的字符串由三部分组成:两个字符串的最长公共子序列LCS + 第一个字符串除去LCS之后的序列 + 第二个字符串除去LCS之后的序列。同一个字符串中的字符的相对顺序不可改变,所以我们可以用字符串与LCS比较来确定字符的相对位置。
此题转化为了先求解LCS,再去构建目的字符串。
LCS部分:
定义 f [i] [j] ** 表示考虑 str1 的前 i 个字符、str2** 的前 j 的字符所形成的最长公共子序列长度。
可得状态转移方程:
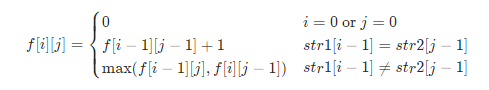
在代码中为了计算方便,在两个string前添加一个空格,令下标从1开始。
构建目的字符串部分:
采用双指针 p、q 分别指向两个string的尾部。
- 当 p 或 q 走完(p == 0 || q == 0),直接将另一字符串剩余部分加入结果中。
- 当指向的两个字符相同时,该字符为LCS中的字符,加入结果,双指针同时自减。
- 根据第一部分得到的状态数组f,判断:
- **f [p] [q] == f [p - 1] [q] **时,str1[p] 加入结果,p–。
- **f [p] [q] == f [p] [q - 1] **时,str2[q] 加入结果,q–。
- 最后,由于是从尾部向前构造,与实际答案相反,因此需要翻转。
代码
class Solution {
public:
string shortestCommonSupersequence(string str1, string str2) {
int m = str1.length(), n = str2.length();
str1 = " " + str1;
str2 = " " + str2;
vector<vector<int>> f(m + 1, vector<int>(n + 1));
for(int i = 1; i <= m; ++i){
for(int j = 1; j <= n; ++j){
if(str1[i] == str2[j]) f[i][j] = f[i-1][j-1] + 1;
else f[i][j] = max(f[i-1][j], f[i][j-1]);
}
}
int p = m, q = n;
string res;
while(p > 0 || q > 0){
if(p == 0) res += str2[q--];
else if(q == 0) res += str1[p--];
else{
if(str1[p] == str2[q]){
res += str1[p--];
q--;
}
else if(f[p][q] == f[p-1][q]) res += str1[p--];
else res += str2[q--];
}
}
return string(res.rbegin(), res.rend());
}
};1550.存在连续三个奇数的数组
题干
给你一个整数数组 arr,请你判断数组中是否存在连续三个元素都是奇数的情况:如果存在,请返回 true ;否则,返回 false 。
示例
示例 1:
输入:arr = [2,6,4,1]
输出:false示例 2:
输入:arr = [1,2,34,3,4,5,7,23,12]
输出:true解法
基本思路:简单的if判断。
代码
class Solution {
public:
bool threeConsecutiveOdds(vector<int>& arr) {
int limit = 0;
for(int num : arr){
if(num % 2) limit++;
else limit = 0;
if(limit > 2)
return true;
}
return false;
}
};1991.找到数组的中间位置
题干
给你一个下标从 0 开始的整数数组 nums ,请你找到 最左边 的中间位置 middleIndex (也就是所有可能中间位置下标最小的一个)。
中间位置 middleIndex 是满足 nums[0] + nums[1] + … + nums[middleIndex-1] == nums[middleIndex+1] + nums[middleIndex+2] + … + nums[nums.length-1] 的数组下标。如果 middleIndex == 0 ,左边部分的和定义为 0 。类似的,如果 middleIndex == nums.length - 1 ,右边部分的和定义为 0 。
请你返回满足上述条件 最左边 的 middleIndex ,如果不存在这样的中间位置,请你返回 -1 。
示例
示例 1:
输入:nums = [2,3,-1,8,4]
输出:3示例 2:
输入:nums = [1,-1,4]
输出:2解法
基本思路:前缀和。
在比较的过程中计算局部前缀和,调用库函数accumulate,相对节约时间和空间一点。
代码
class Solution {
public:
int findMiddleIndex(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0);
int preSum = 0;
for(int i = 0; i < nums.size(); ++i){
if(sum - nums[i] == 2 * preSum)
return i;
preSum += nums[i];
}
return -1;
}
};2023.3.29
1641.统计字典序元音字符串的数目
题干
给你一个整数 n,请返回长度为 n 、仅由元音 (a, e, i, o, u) 组成且按 字典序排列 的字符串数量。
字符串 s 按字典序排列需要满足:对于所有有效的 i,s[i] 在字母表中的位置总是与 s[i+1] 相同或在 s[i+1] 之前。
示例
示例 1:
输入:n = 1
输出:5示例 2:
输入:n = 2
输出:15解法
基本思路:动态规划。


代码
class Solution {
public:
int countVowelStrings(int n) {
vector<vector<int>> f(n, vector<int>(5));
for(int i = 0; i < 5; ++i)
f[0][i] = 1;
for(int i = 1; i < n; ++i)
for(int j = 0; j < 5; ++j)
for(int k = 0; k <= j; ++k)
f[i][j] += f[i - 1][k];
int res = 0;
for(int i = 0; i < 5; ++i)
res += f[n - 1][i];
return res;
}
};优化
空间优化:二维数组 ——> 一维数组。
因为最终要求的实际是 n - 1 处的前缀和,过程中的值并不需要,因此可以省略二维数组中的第一维(i),通过直接修改的的方式不断更新一维数组的值直到 n - 1。
class Solution {
public:
int countVowelStrings(int n) {
int f[5] = {1, 1, 1, 1, 1};
for(int i = 0; i < n - 1; ++i){
int sum = 0;
for(int j = 0; j < 5; ++j){
sum += f[j];
f[j] = sum;
}
}
int res = 0;
for(int i = 0; i < 5; ++i)
res += f[i];
return res;
}
};15.三数之和
题干
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。
请你返回所有和为 0 且不重复的三元组。
注意,输出的顺序和三元组的顺序并不重要。
示例
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]示例 2:
输入:nums = [0,1,1]
输出:[]解法
基本思路:排序 + 双指针。
考虑到和为0,三数之中必有正负或全0,且顺序不重要,那么先排个序肯定方便计算。
三个数,考虑用三个指针,其中for循环指针指定最左侧的数,从左往右遍历,那么剩下双指针只需要考虑该数右侧的部分即可(避免重复)。
双指针指向该数右侧子数组的两端,分别向中间移动判断。
需要注意的去重情况有:
- 当最左侧数大于0时,右侧两数也大于0,sum必大于0,直接结束循环。
- 当最左侧数 nums [i] == nums [i - 1] 时,此时双指针移动得到的三元组是一样的,跳过。
- 同上,当左指针 nums[l] == nums[l + 1] 时,三元组重复,跳过,l++。
- 当右指针 nums[r] == nums[r + 1] 时,三元组重复,跳过,r–。
去重后,根据sum的值大于或小于0判断移动右指针还是左指针。
代码
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(), nums.end());
for(int i = 0; i < nums.size(); ++i){
int l = i + 1, r = nums.size() - 1;
if(nums[i] > 0)
break;
if(i > 0 && nums[i] == nums[i - 1])
continue;
while(l < r){
int sum = nums[i] + nums[l] + nums[r];
if(sum == 0){
while(l < r && nums[l] == nums[l + 1]) l++;
while(l < r && nums[r] == nums[r - 1]) r--;
res.push_back({nums[i], nums[l++], nums[r--]});
}
else if(sum > 0)
r--;
else
l++;
}
}
return res;
}
};16.最接近的三数之和
题干
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。返回这三个数的和。
假定每组输入只存在恰好一个解。
示例
示例 1:
输入:nums = [-1,2,1,-4], target = 1
输出:2示例 2:
输入:nums = [0,0,0], target = 1
输出:0解法
基本思路:排序 + 双指针。
同15题思路:排序肯定方便计算。三个数三个指针,其中for循环指针指定最左侧的数,从左往右遍历,那么剩下双指针只需要考虑该数右侧的部分即可(避免重复)。双指针指向该数右侧子数组的两端,分别向中间移动判断。
不需要去重,只用计算和与target比较,根据大小判断移动哪个指针;
维护结果变量res,如果 和与target的差值 小于 res与target的差值,就更新res为本次的和。
代码
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
int res = nums[0] + nums[1] + nums[2];
sort(nums.begin(), nums.end());
for(int i = 0; i < nums.size(); ++i){
int l = i + 1, r = nums.size() - 1;
while(l < r){
int sum = nums[i] + nums[l] + nums[r];
if(abs(target - sum) < abs(target - res))
res = sum;
if(sum > target)
r--;
else if(sum < target)
l++;
else
return res;
}
}
return res;
}
};18.四数之和
题干
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
- 0 <= a, b, c, d < n
- a、b、c 和 d 互不相同
- nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
示例
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]示例 2:
输入:nums = [2,2,2,2,2], target = 8
输出:[[2,2,2,2]]解法
基本思路:排序 + 双指针。
思路同15.三数之和,无非外面多加了层循环。
需要注意的去重情况有:
- 当最左侧数 nums [i] == nums [i - 1] 时,此时双指针移动得到的四元组是一样的,跳过。
- 当左侧第二个数 nums [j] == nums [j - 1] 时,此时双指针移动得到的四元组是一样的,跳过。
- 同上,当左指针 nums[l] == nums[l + 1] 时,四元组重复,跳过,l++。
- 当右指针 nums[r] == nums[r + 1] 时,四元组重复,跳过,r–。
去重后,根据sum的值大于或小于0判断移动右指针还是左指针。
注意越界问题,sum使用 long 记录。
代码
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> res;
sort(nums.begin(), nums.end());
for(int i = 0; i < nums.size(); ++i){
if(i > 0 && nums[i] == nums[i - 1])
continue;
for(int j = i + 1; j < nums.size(); ++j){
int l = j + 1, r = nums.size() - 1;
if(j > i + 1 && nums[j] == nums[j - 1])
continue;
while(l < r){
long sum = (long)nums[i] + nums[j] + nums[l] + nums[r];
if(sum == target){
while(l < r && nums[l] == nums[l + 1]) l++;
while(l < r && nums[r] == nums[r - 1]) r--;
res.push_back({nums[i], nums[j], nums[l++], nums[r--]});
}
else if(sum > target)
r--;
else
l++;
}
}
}
return res;
}
};2023.3.30
1637.两点之间不包含任何点的最宽垂直区域
题干
给你 n 个二维平面上的点 points ,其中 points[i] = [xi, yi] ,请你返回两点之间内部不包含任何点的 最宽垂直区域 的宽度。垂直区域 的定义是固定宽度,而 y 轴上无限延伸的一块区域(也就是高度为无穷大)。 最宽垂直区域 为宽度最大的一个垂直区域。
请注意,垂直区域 边上 的点 不在 区域内。
示例
示例 1:
输入:points = [[8,7],[9,9],[7,4],[9,7]]
输出:1示例 2:
输入:points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
输出:3解法
基本思路:排序。
其实就是求所有点 x 坐标之间的最大差值。按第一位排序,然后求最大差值即可。
代码
class Solution {
public:
int maxWidthOfVerticalArea(vector<vector<int>>& points) {
sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] < b[0];
});
int res = 0;
for(int i = 1; i < points.size(); ++i)
res = max(res, points[i][0] - points[i-1][0]);
return res;
}
};优化

class Solution {
public:
int maxWidthOfVerticalArea(vector<vector<int>>& points) {
int n = points.size();
vector<int> nums;
for (auto& p : points) {
nums.push_back(p[0]);
}
const int inf = 1 << 30;
int mi = inf, mx = -inf;
for (int v : nums) {
mi = min(mi, v);
mx = max(mx, v);
}
int bucketSize = max(1, (mx - mi) / (n - 1));
int bucketCount = (mx - mi) / bucketSize + 1;
vector<pair<int, int>> buckets(bucketCount, {inf, -inf});
for (int v : nums) {
int i = (v - mi) / bucketSize;
buckets[i].first = min(buckets[i].first, v);
buckets[i].second = max(buckets[i].second, v);
}
int ans = 0;
int prev = inf;
for (auto [curmin, curmax] : buckets) {
if (curmin > curmax) continue;
ans = max(ans, curmin - prev);
prev = curmax;
}
return ans;
}
};704.二分查找
题干
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1解法
基本思路:二分查找。
当二分查找的双指针是闭区间 [ l, r ] 时while中判断是 <= ;当左闭右开时,while中使用 < ,**r = num.size()**。
代码
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while(l <= r){
int mid = (l + r) / 2;
if(nums[mid] == target)
return mid;
else if(nums[mid] > target)
r = mid - 1;
else
l = mid + 1;
}
return -1;
}
};35.搜索插入位置
题干
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。
示例
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2示例 2:
输入: nums = [1,3,5,6], target = 7
输出: 4解法
基本思路:二分查找。
和704.二分查找一样,最后return的值改成双指针相遇的位置,就是应该插入的位置。
代码
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while(l <= r){
int mid = (l + r) / 2;
if(nums[mid] < target) l = mid + 1;
else if(nums[mid] > target) r = mid - 1;
else return mid;
}
return l;
}
};34.在排序数组中查找元素的第一个和最后一个位置
题干
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target,返回 **[-1, -1]**。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]解法
基本思路:二分查找。
需要两次二分查找,找左边的就不断将右指针向左压缩,找到target后继续压缩直至左右指针重合,找右边同理。
代码
class Solution {
public:
int findRange(vector<int>& nums, int target, bool isLeft){
int l = 0, r = nums.size() - 1;
int res = -1;
while(l <= r){
int mid = (l + r) / 2;
if(nums[mid] < target) l = mid + 1;
else if(nums[mid] > target) r = mid - 1;
else{
res = mid;
if(isLeft) r = mid - 1;
else l = mid + 1;
}
}
return res;
}
vector<int> searchRange(vector<int>& nums, int target) {
return {findRange(nums, target, true), findRange(nums, target, false)};
}
};69.x的平方根 、367.有效的完全平方数
题干
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例
示例 1:
输入:x = 4
输出:2示例 2:
输入:x = 8
输出:2解法
基本思路:二分查找。
小数部分舍去,因此结果的平方必然 小于等于 x,因此在该处记录mid值,等到 l 和 r 重合后的mid即为结果。
注意用 long long 存储平方结果。
代码
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x, res;
while(l <= r){
int mid = (l + r) / 2;
if((long long)mid * mid <= x){
l = mid + 1;
res = mid;
}
else r = mid - 1;
}
return res;
}
};27.移除元素、26.删除有序数组中的重复项
解法
基本思路:双指针。
利用了题意只打印前返回值个数的元素且不在意顺序,因此不需要真删,最后返回头指针的位置即可。
代码
// 27
class Solution {
public:
// 双指针
int removeElement(vector<int>& nums, int val) {
int l = 0, r = nums.size() - 1;
while(l <= r){
if(nums[l] == val)
nums[l] = nums[r--];
else
l++;
}
return l;
}
// vector方法操作
int removeElement2(vector<int>& nums, int val) {
if(nums.empty()) return 0;
vector<int>::iterator it = nums.begin();
while(it != nums.end()){
if(*it == val)
nums.erase(it);
else
it++;
}
return nums.size();
}
};// 26
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int l = 0;
for(int r = 0; r < nums.size(); ++r){
if(nums[l] != nums[r])
nums[++l] = nums[r];
}
return l + 1;
}
};283.移动0
解法
基本思路:双指针。
确保 r指针 的左边均为非0值,l指针 用于遍历一遍,将所有非0值与 r 所在位置交换。
代码
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int r = 0;
for(int l = 0; l < nums.size(); ++l)
if(nums[l])
swap(nums[l], nums[r++]);
}
};844.比较含退格的字符串
解法
基本思路:双指针。
慢指针维护真实的字符串,始终指向真实字符串的后一位(相当于真实字符串的长度)。
快指针用于遍历。非 ‘#’ 时,将快指针指向的字符赋给慢指针位置,慢指针右移;当为 ‘#’ 时,不赋值并慢指针后退。最后慢指针用于截取字符串(前slow个字符)。
代码
class Solution {
public:
string strBack(string s){
int slow = 0;
for(int fast = 0; fast < s.length(); ++fast)
if(s[fast] != '#')
s[slow++] = s[fast];
else if(slow > 0)
slow--;
return s.substr(0, slow);
}
bool backspaceCompare(string s, string t) {
return strBack(s) == strBack(t);
}
};977.有序数组的平方
解法
基本思路:双指针。
其实是三指针。
维护一个指针truth指向结果数组的尾部。另外双指针分别指向头尾,将两者中平方更大的数加入结果数组(同时truth指针左移,因为从大到小插入),指针向中间移动。
代码
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int truth = nums.size() - 1;
vector<int> res(nums.size());
for(int i = 0, j = nums.size() - 1; i <= j;){
if(nums[i] * nums[i] < nums[j] * nums[j]){
res[truth--] = nums[j] * nums[j];
j--;
}
else{
res[truth--] = nums[i] * nums[i];
i++;
}
}
return res;
}
};2023.3.31
2367.算术三元组的数目
解法
基本思路:哈希表。
因为严格递增,可以用哈希表存储整个数组,然后遍历找另外两个值是否在哈希表中。
代码
class Solution {
public:
int arithmeticTriplets(vector<int>& nums, int diff) {
unordered_set<int> res;
int cnt = 0;
for(int c : nums)
res.emplace(c);
for(int c : nums){
if(res.find(c + diff) != res.end() && res.find(c + diff * 2) != res.end())
cnt++;
}
return cnt;
}
};209.长度最小的子数组
题干
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2示例 2:
输入:target = 4, nums = [1,4,4]
输出:1解法
基本思路:双指针、滑动窗口。
依旧是快慢指针,快指针完成一次数组遍历,并累加和至sum中。
每次累加后判断sum与target,若 ≥ ,则记录此时长度,同时慢指针移动,sum减去值,直至小于target。
代码
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int slow = 0, fast = 0;
int res = INT_MAX, sum = 0;
for(; fast < nums.size(); ++fast){
sum += nums[fast];
while(sum >= target){
res = min(res, fast - slow + 1);
sum -= nums[slow++];
}
}
return res == INT_MAX ? 0 : res;
}
};904.水果成篮
题干
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
- 你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
- 你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
- 一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。
示例
示例 1:
输入:fruits = [1,2,3,2,2]
输出:4示例 2:
输入:fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出:5解法
基本思路:双指针、滑动窗口、哈希表。
依旧是快慢指针,快指针完成一次数组遍历,用哈希表记录已采摘的每种水果的数量。
当种类数大于2时,将慢指针所指种类的水果数量减1(减至0时将该种类从哈希表中删除),并移动慢指针。
更新每次移动快指针后的最大长度。
代码
class Solution {
public:
int totalFruit(vector<int>& fruits) {
unordered_map<int, int> types;
int res = 0;
int slow = 0, fast = 0;
for(;fast < fruits.size(); ++fast){
types[fruits[fast]]++;
while(types.size() > 2){
int ex = fruits[slow++];
if(--types[ex] == 0)
types.erase(ex);
}
res = max(res, fast - slow + 1);
}
return res;
}
};76.最小覆盖子串
题干
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"示例 2:
输入:s = "a", t = "a"
输出:"a"解法
基本思路:双指针、滑动窗口、哈希表。
典型的滑动窗口思路,窗口扩展时寻找可行解,窗口收缩时优化可行解。
- 先用哈希表存储 t 串中每种字符的数量,设立双指针。
- 不断右移快指针,增大滑动窗口,直至包含 t 中所有字符。
- 右移慢指针,去除不需要的元素,直至遇到一个必须包含的字符,记录最小长度和起始位置。
- 慢指针右移一位,此时条件不满足,从步骤2继续执行,直至快指针超出 s 的范围。
以上思路遇到的问题:
如何判断窗口内包含了 t 中所有字符?
步骤1的哈希表,每当快指针增加一个所需字符时,哈希表对应数量减1,慢指针加1。存在负数的情况,因为当添加某个字符数量超过需求时,若窗口压缩时去除了多余的该字符依旧是符合要求的。当哈希表中所有键对应的值均≤ 0 时,表示包含了全部所需字符。
每次判断都要遍历哈希表?
维护一个变量 needChar 表示所需元素的总数,窗口每次添加所需字符时,哈希表中对应的值和 needChar 同时减1。当 needChar == 0 时,已达标可以进行缩减了。
没有符合要求的子串和全部字符才符合要求这两种情况的区分?
一开始 minLen 初值设置为 s.length(),发现无法区分这两种情况。修改为 INT_MAX 即可,return时根据 minLen 是否被修改过作出选择。
关于unordered_map
有个注意的点是,当执行 sub[c] > 0 时若map中不存在键c,会生成一个 **sub[c] = 0 **的键值对,因此我通过 在该判断前先判断是否存在该键 来解决,不知是否有更简便的方法TODO。
代码
class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char, int> sub;
for(char c: t)
sub[c]++;
int slow = 0, fast = 0;
int minLen = INT_MAX, minLoc = 0, needChar = t.length();
for(; fast < s.length(); ++fast){
int c = s[fast];
if(sub.count(c) && sub[c]-- > 0)
needChar--;
if(needChar == 0){
while(sub.count(s[slow]) == 0 || sub[s[slow]] < 0){
if(sub.count(s[slow]))
sub[s[slow]]++;
slow++;
}
if(minLen > fast - slow + 1){
minLen = fast - slow + 1;
minLoc = slow;
}
sub[s[slow++]]++;
needChar++;
}
}
return minLen > s.length() ? "" : s.substr(minLoc, minLen);
}
};59.螺旋矩阵 Ⅱ
题干
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例
示例 1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]解法
基本思路:模拟过程。
因为是正方形,因此会规律很多。每轮循环计算一圈边界,无论横纵都遵循左闭右开的走法,如下图,即可避免重复。
若 n 为奇数,最中间的值需要单独补充。
代码
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> mat(n, vector<int>(n));
int loop = n / 2;
int sx = 0, sy = 0;
int num = 0, cnt = 1;
int i, j;
while(loop--){
for(j = sy; j < n - cnt; ++j)
mat[sy][j] = ++num;
for(i = sx; i < n - cnt; ++i)
mat[i][j] = ++num;
for(; j > sy; --j)
mat[i][j] = ++num;
for(; i > sx; --i)
mat[i][j] = ++num;
sx++;
sy++;
cnt++;
}
if(n % 2)
mat[n / 2][n / 2] = n * n;
return mat;
}
};

